Астана 2014
Л.Н: Гумилев атындағы Еуразия ұлттық университетiнiң жалпы және теориялық физика кафедрасының 28.08.2014 жылғы отырысында қаралып мақұлданған
Дайындағандар: Алтеев Ж., Азимханова А.М.,Сагидуллаева Ж.М.,Балабеков Қ.Н.
Жалпы физика курсы бойынша зертханалық жұмыстар. Оқу-әдістемелік құралы. Л.Н.Гумилев атындағы Еуразия ұлттық университеті. Астана, 2014. – 67 бет.
Оқу-әдістемелік құралында бағдарламаға сәйкес жалпы физика курсынан 14 зертханалық жұмыстың әдістемелік нұсқаулары қазақ тілінде берілген. Нұсқауларда жұмыстың теориясынан қысқаша мәлімет, қондырғылардағы жұмыстың орындалу тәртібі, есептеу формулалары, жұмысты тапсыруға арналған сұрақтар тізімі келтірілген. Оқу-әдістемелік құралы жоғары оқу орындарының жаратылыстану және техникалық бағытындағы студенттеріне арналған.
Мазмұны
1.Пәннің жалпы сипаттамасы……..................………….......................................................5
2. Өлшеу қателіктері……............………...……………………………………….................5
3. № 1 Зертханалық жұмыс. Заттардың тығыздығын анықтау……….….........................12
4. № 2 Зертханалық жұмыс. Баллистикалық маятник көмегімен оқтың ұшу
жылдамдығын анықтау…………………………………………………..............................15
5. № 3 Зертханалық жұмыс. Обербек маятнигінің көмегімен қатты дене айналмалы қозғалыс динамикасының негізгі заңын зерттеу………………….....................................18
6. № 4 Зертханалық жұмыс. Маховиктік дөңгелек.............................................................21
7. № 5 Зертханалық жұмыс. Маятниктер тербелісі………….............................................23
8. № 6 Зертханалық жұмыс. Ауа молекуласының жылу өткізгіштік
коэффициентін анықтау………………...…………............................................................ 28
9. № 7 Зертханалық жұмыс. Қатты денені қыздыру және балқыту кезіндегі
энтропияның өзгеруін анықтау……………………………………………………….…....32
10. №8 Зертханалық жұмыс. Қатты дененің сызықтық ұлғаю
коэффициентін анықтау……………………………………………………….…................38
11. № 9 Зертханалық жұмыс. Резистивтік сымның кедергісін анықтау………..……....40
12. № 10 Зертханалық жұмыс. Жердің магнит өрісі индукция векторының
горизонталь құраушысын анықтау……………….………..................................................45
13. № 11 Зертханалық жұмыс.Микроскоп көмегімен шынының сыну
көрсеткішін анықтау….…………….…….............................................................................49
14. № 12 Зертханалық жұмыс. Жұқа линзаның фокус аралығын анықтау……………...55
15. № 13 Зертханалық жұмыс. Дифракциялық тордың көмегімен жарық
толқынының ұзындығын анықтау …………………….…..................................................59
16. № 14 Зертханалық жұмыс. Ішкі фотоэффектіні оқып үйрену..………………………64
17. Әдебиеттер……………...…………………………………………….…....................68
ПӘННІҢ ЖАЛПЫ СИПАТТАМАСЫ
1.Пәнді меңгерудің мақсаты мен міндеттері.
Мақсаты:
1.Физикалық қондырғылардың көмегімен физикалық тәжірибелер жүргізудің және өлшеу нәтижелерін өңдеудің машықтығын қалыптастыру.
2.Алынған білімдерін жалпы кәсіби пәндерді, сонымен бірге оқыту бағытындағы арнайы пәндерді меңгеруге қолдану.
Міндеттері:
1.Физиканың әмбебап заңдарын білудің нәтижесінде физикалық құбылыстар мен процестерді зерттеу әдістерін қоюды және өткізуді үйрету.
2.Әр түрлі физикалық процестер мен құбылыстарды оқып үйренуде заманауи қондырғылар мен әр түрлі есептеуіш құралдарын қолдануды үйрету.
3.Тәжірибе нәтижелерін қарапайым математикалық есептеулермен бірге компьютерлік техниканың және автоматтандырылған жүйелерді қолдана отырып өңдеуді үйрету.
2.Бакалавриаттың құрылымдық оқу бағдарламасындағы
пәннің алатын орны.
Физика табиғат құбылыстарының жалпы заңдылықтарын, материяның құрылысы мен қасиетін, оның қозғалыс заңдарын қарастыратын ғылым. Сондықтан физиканың түсініктері және оның заңдары бүкіл жаратылыстану ғылымдарының негізінде жатыр. Физиканы басқа жаратылыстану ғылымдарынан бөлетін шекара шартты түрде ғана және уақыттың өтуімен өзгеріп отырады.
Физика негізінде – тәжірибелік ғылым, оның заңдары тәжірибе жүзінде тағайындалған фактілерге сүйенеді. Бұл заңдар сандық қатынас түрінде болып, математикалық түрде сипатталады. Кез келген құбылысты оқып үйренгенде тәжірибе мен теория бірдей өлшемде керек және өзара байланысты. Физика материалдармен және техникамен байланысты ғылымның және барлық жаратылыстану бағытындағы пәндерден бакалавр дайындаудағы негізгі пән болып табылады.
Зертханалық сабақтар арнайы жабдықталған зертханаларда өтіледі. Әрбір зертханалық жұмыста мынадай бөлімдер бар: жұмыстың мақсаты; қажетті құрал-жабдықтар; теориядан қысқаша мәлімет; тәжірибелік қондырғының сипаттамасы; жұмыстың орындалу реті; өлшеу нәтижелерін өңдеу; бақылау сұрақтары.
3.өлшеу қателіктері
Барлық өлшеулер қаншалықты ұқыпты жүргізілгенімен тек жуық нәтиже береді, себебі кез келген өлшеу қателіксіз болмайды.
Қандай да бір х физикалық шама n рет өлшенді дейік, нәтижесінде осы шаманың х1, х2,… хn мәндері алынсын. Өлшеуді орындаған кезде, нәтижені анықтап қана қоймай, оның дәлдігі жайлы білу керек. Көптеген жағдайларда х шамасының өлшем мәндері х1, х2… хn болғанда, бұл өлшеудің орташа арифметикалық нәтижесі <х> болып табылады. Бұл кезде өлшенген шама мәнінің интервалын ±Dx көрсету қажет;
<х> +Dx - өлшенген шаманың мүмкін үлкен мәні; <х>-Dx – мүмкін кіші мәні.
Dx шамасы өлшеу нәтижесінің қателігі немесе абсолюттік қателік деп аталады, ал <х>+Dx интервалы мен <х>-Dx интервалына дейінгі аралық сенімділік интервалы деп аталады. <х> - орташа мәнінің шын мәнінен айырмашылығы, ол Р-ның сәйкес болуынан шығады. Ол бір тектес өлшеу түрлерінің нәтижелерінің үлесіне тең, яғни Dx шамасының оның шын мәнінен айырмашылығы сандық мәнінде болады. Сенім аралығы e- берілген Р сенімділік ықтималдылығы бойынша, <х> нүктесінде кесіндінің 2e сандық осі центрмен бірге өлшенетін х шаманың мәнін өзіне қосу арқылы анықталады.
Анықтаушы Р0 сенімділік ықтималдылығы үшін өлшеу қателіктері болып табылады. Өлшенген нәтиже шаманың шын мәніне сәйкес келуі үшін үлкен Р сенімділік ықтималдылығы алынады. Бұл жағдайда, ±e =kDx интервалының аралығында қалыптасады, мұнда k коэффициенті Р/Р0 қатынасы бойынша анықталады.
k = Р/Р0
Егер құралдың көрсетуі бойынша өлшеу нәтижелерін қайта жөндеп, көп немесе аз қателіктерін тапсақ, онда өлшеудің жөнделген нәтижелерінің орташа арифметикалық мәні мына формула бойынша табылады:
Әдетте жалпы қабылданған өлшеудің стандарт қателіктерінің орнына орташа квадраттық қателіктер алынады. Ол өлшеу қателіктерінің жақсы жуықтайтын кездейсоқ шамалары үшін Гаусс анықтамасының дисперсиясына тең.
Өлшеу нәтижесінің орташа арифметикалық мәнінен алынған орташа квадраттық ауытқу мына формуламен анықталады:
Орташа квадраттық қателіктің ауытқуы S<x> шамасының орташа арифметикалық қателігін <x> түсіндіреді.
түріндегі жазу сондай дәлдікпен алынған <х> - тің кез келген барлық өлшеуінің 68% 
, 
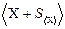аралығына келетіндігін көрсетеді. Басқаша айтқанда алынған нәтиже дұрыс нәтижеден Р=68% сенімділік ықтималдығымен 
аралығында болады. Өлшеу нәтижесінің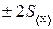 
аралықтарында болу ықтималдығы 95,4%, ал 
- 99,7% болады.
Өлшеу қателіктері Гаустың үлестірілуімен тек шексіз үлкен өлшеулер санына сәйкес келеді. Аз өлшеулерде өлшеу нәтижесінің кездейсоқ қателігінің сенім аралығын есептеуде Стьюдент үлестірілуі қолданылады:
e=±tp.n S<x>
мұндағы, ±tp.n- n рет өлшеу саны үшін және Стьюдент коэффициентінің кестесі арқылы Рсенімділік ықтималдылығымен анықталатын Стьюдент коэффициенті.
Стьюдент коэффициенттерінің кестесі.
Р – сенімділік ықтималдылығы.n - өлшеулер саны.
| n\P | 0,5 | 0,6 | 0,7 | 0,8 | 0,09 | 0,95 | 0,0989 | 0,999 |
| 0,82 0,77 0,74 0,73 0,72 0,71 0,71 0,70 0,69 0,69 0,68 0,68 0,68 0,67 | 1,38 1,06 0,98 0,94 0,92 0,90 0,90 0,90 0,88 0,87 0,86 0,85 0,85 0,85 0,84 | 2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,0 1,0 1,00 | 3,1 1,9 1,6 1,5 1,5 1,4 1,4 1,4 1,4 1,3 1,3 1,2 1,3 1,3 1,3 | 6,3 2,9 2,4 2,1 2,0 1,9 1,9 1,9 1,8 1,8 1,7 1,7 1,7 1,7 1,6 | 12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 2,1 2,1 2,0 2,0 2,0 2,0 | 31,8 7,0 4,5 3,7 3,4 3,1 3,00 2,9 2,8 2,6 2,5 2,4 2,4 2,4 2,3 | 636,6 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 4,1 3,9 3,6 3,5 3,4 3,3 |
Кестеден көрініп тұрғандай, 5-7 рет өлшеу үшін де және шексіз көп рет өлшеу кезінде де орташа квадраттық қателіктерді қолдануға болады. Автоматты өлшеу кезінде өлшеу саны өте үлкен болуы мүмкін, алайда өлшеу санының артуы орташа квадраттық қателіктердің азаюына әкелгенімен, қателік интервалы аралығында сенім ықтималдылығын өзгертпейді.
Қателіктерді жүйелі және кездейсоқ деп екі түрге бөлуге болады. Олардың арасындағы айырмашылық: жүйелі қателіктер шамасы және таңбасы жағынан тұрақты, ал кездейсоқ қателіктер, керісінше, өзінің шамасы мен таңбасын өзгертіп тұрады. Кездейсоқ қателіктерді көп рет өлшеу арқылы кемітуге болады. Жүйелі қателікті мұндай жолмен кеміту мүмкін емес. Кездейсоқ қателікті статистикалық әдістермен өңдеуге болады, ал жүйелі қателіктерге бұл әдістер қолданылмайды.
Жүйелі қателіктер өлшеу қондырғыларының қателіктерінен пайда болады (дұрыс істемейтін секундомер, қисық сызғыш, тілшесі бар құрал, яғни тілшесі өлшеу алдында нөлге келтірілмеген), тәжірибені жүргізу шартының алдын ала дайындалған теориядан айырмашылығынан, тәжірибе әдістемесінің жеткіліксіз болуынан пайда болады.
Жүйелі қателіктерді анықтау үшін ешқандай жалпы ереже жоқ. Олардың әр түрлі жағдайда пайда болуы арнайы зерттеулерді қажет етеді, сондықтан жүйелі қателіктерді толығымен ескермеуге болмайды, оларды тек кездейсоқ қателіктер тобына ауыстыруға болады.
Кездейсоқ қателіктер тәжірибелерде әр уақытта болады және ол көп мөлшердегі факторлар қосынды әсерлерінің нәтижесі болып табылады, ал олардың әрқайсысының әсерін ескеру мүмкін емес. Кездейсоқ қателіктерді тудыру көздері: бақылаушының аз ғана қателігі, қондырғыға әсер ететін кездейсоқ әсерлер және басқалар. Кездейсоқ қателіктерді алып тастауға болмайды, бірақ олардың ықпалын көп өлшеулер көмегімен нәтижелерін математикалық өңдеу арқылы ескеруге болады.
Кездейсоқ қателіктің түрлілігі – өрескел қателік немесе байқамай қалатын қателік болып бөлінеді. Олар тәжірибе жүргізушінің анық зер салмауынан болады (мысалы, өлшеуіш құрал арқылы дұрыс өлшемеу, санақты дұрыс жазбау және т.с.с.) Көп жағдайда, байқамай жіберілетін қателіктер көп ретті өлшеулер кезінде анық білінеді, себебі сәйкес санаудың басқалардан айырмашылықтары болады. Нәтижені қайта өңдеген кезде ондай санауды алып тастау керек.
Жүйелі қателіктерді ескере отырып, өлшеу нәтижесінің жалпы қателігінің сенім аралығын былай жазамыз:
мұндағы q - жүйелі қателік, бұл оқу зертханасындағы өлшеуіш құралдың шкаласы бөліктерінің құнымен бағаланады немесе өлшеуіш құралда көрсетіледі.
Кейбір жағдайларда жалпы қателіктердің сенім аралығы мына формула бойынша есептеледі:
Өлшеудің соңғы нәтижесін мына түрде жазамыз: х=<x>±Dх;
Мысалы, r= (7,70±0,72) 103 кг/м3, P=0,95.
Өлшеудің сан мәнінің сандық реті Dх сенім аралығын анықтаушы нәтижелерінің сандық ретімен бірдей болуы тиіс. Сенім аралығы екі мәндік санмен жазылады.
Өлшем дәлдігін білдіретін өлшеу нәтижесінің салыстырмалы қателігі мынаған тең:
Жанама өлшеу нәтижелерінің қателіктерін бағалау
Ізделініп отырған шама мына формула бойынша анықталады:
<y> = f (<x1>, <x2>,….<xn>)
Бұған өлшенетін шаманың орташа мәні қойылатын болады.
Жанама өлшеудің абсолют қателігі, әдетте, функцияның толық дифференциалын табу ережесімен анықталады. Мұнда айнымалылар дифференциялдары орнына алынған қателіктердің мәні қойылады. Бұл жағдайда барлық «-» теріс белгісі дифференциалдық формулада «+»оң болып ауыстырылады. Мысалы, жанама өлшенген шама
у = 
(х 
,х2,...z1,. z2..)
мұндағы, х1, х2, … өлшенетін шамалар,
z1, z2… - белгілі шамалардың қабылданған кестелік мәндері.
Сонда абсолют қателік мынаған тең:
Dy=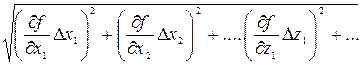 
Кестелік мәндер қателіктері орнына соңғы сан мәнінің жартысы алынады, әдетте бұл шама өлшеу қателігінен көп аз болады, оны ескермеуге болмайды.
Салыстырмалы қателік тікелей өлшеулердегідей абсолют қателіктің өлшенетін шамасына қатынасы арқылы анықталады. Алайда абсолют қателіксіз–ақ, салыстырмалы қателікті табуға болады. Бұл үшін:
1. есептеу формуласын y= f (x1, x2…xn) логарифмдейміз;
2. lny – тен толық дифференциалды табамыз.
d(lny)= 
lny=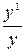 
туындысы және 
дифференциалы барлық өлшеулер бойынша салыстырмалы қателіктердің қосындысын береді.
Жанама өлшеудің салыстырмалы қателігі тікелей өлшеулердің салыстырмалы қателіктерінің қосындысы түрінде анықталады:
= 
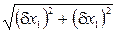
Бастапқы қателіктер тәуелсіз және кездейсоқ болса, онда жанама өлшеулер қателіктерін есептеуде, олардың квадраттық қосындысы алынады.
Соңғы нәтиже мына түрде жазылады:
y =<y>±Dy;
Басқа шамалардың қарапайым функция болып табылатын шамаларының қателіктерін табу үшін кейбір формулалар кестеде келтірілген.
Жанама өлшеулердің салыстырмалы қателіктерінің кестесі
| Функция түрі | Абсолют қателік | Салыстырмалы қателік |
| X,Y,Z | 
| 
|
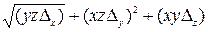
| x/y | 
| 
|
| 
| 
|
| 
| 
|
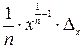
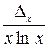
Графиктерді салу және өңдеу ережесі
Графиктер өлшемі дәптер парағынан кем емес миллиметрлік қағазға салынады. Миллиметрлік қағазға қарындашпен координаттық осьтер сызылады, тәуелсіз шама үшін абсцисса осі таңдап алынады. Осьтердің ұштарына физикалық шамалардың белгіленуі мен олардың өлшем бірліктері көрсетіледі.
Масштаб бөліктері осьтерде 1, 2, 5 …сандарына еселі немесе 10±n санына көбейтілген (n– бүтін сан), бірдей қашықтықтарда орналасқан «бүтін» сандар түрінде салынады.
График барлық жерді алып жатуы үшін, осьтер бойында орналасатын санақ басы мен масштабты дұрыс таңдап алу керек. Таңдаудан кейін миллиметрлік қағазға қарындашпен осьтер және масштаб бойынша санақ басында майыспайтын және сынбайтын қисықтармен жалғанған тәжірибелік нүктелер салынады.
Қисық берілген нүктелерге жақын өтуі керек, бірақ оны әр нүкте сайын өткізуге тырыспау керек. Қисықтың екі жағы бойынша бірдей нүкте сандары орналастырылу керек.
Тәжірибелерде екі өлшемді шамалардың, x және y сызықтық тәуелділігі жиі кездеседі.
у=кх +b,
мұндағы, k және b – тұрақты шамалар.
Мұндай тәуелділік сызбасы түзу сызық түрінде болады. Тәжірибелік нүктелер әр түрлі қателіктер әсерінен бір түзуде жатпайды. Зерттеуді жүргізушінің мақсаты – ең тиімді жолмен түзуді жүргізу және тангенс бойынша көлбеу бұрышты анықтау.
Көп жағдайда, бұл коэффициенттің шамасының анықталуы тәжірибенің басты мақсаты болып табылады.
Таразыда өлшеу ережесі
Массаларды анықтау үшін дәлдігі және өлшеу аралықтары әр түрлі таразылар қолданылады. Таразылар әдетте, дәлдігі бірнеше миллиграмдар құратын техникалық таразылар және дәлдігі миллиграмның жүздік немесе мыңдық үлесін құрайтын электрондық таразылар болып бөлінеді. Таразылар қатаң түрде өлшенуге дайын болуы керек. Таразыны өлшеуге дайындауда жіберілген кез келген өрескелдік таразы тілінің тік бағытынан ауытқуына және өлшеу кезінде жүйелі қателердің пайда болуына әкеледі. Жүк өлшенбеген кезде таразы тілі тігінен нөлдік күйдің жанында тұрады. Бұл кезде таразы тілі нөлдік санмен сәйкес келмейді, сондықтан өлшеу алдында таразы тілін нөлге әкелу керек және шкаланың бөліктерін анықтау керек.
Таразылардағы жүкті өзгертуге болады. Өлшенетін денені арнайы қысқыш арқылы алу керек. Таразыны дұрыс орналастырмайынша, толығымен арретирді босатпау керек.
Таразылардағы жүйелі қателерді болдырмау мына әдістер үшін қолданылады:
1. Екі рет өлшеу әдісі. Дене алдымен таразының бір табақшасында, сосын басқа табақшасында өлшенеді. Нәтижесі екі өлшеудің орташа арифметикалық шамасы болып табылады.
2. Салыстыру әдісі. Дене әдеттегі құммен тең өлшеніп, таразының екінші табақшасына салынады. Осыдан кейін дене алынып тасталады да, әр түрлі салмақты кірлермен ауыстырылады.
3. Тұрақты тиелмелі әдіс. Мұнда бірінші табақшада тұрақты кір тұрады, ол кірдің массасы өлшеніп жатқан дене массасынан артық, екінші табақшада әр түрлі салмақтағы кірлер болады. Олар кірлер тепе-теңдігін қамтамасыз етеді. Сосын екінші табақшаға өлшенетін денені салады да, әр түрлі салмақты кірдің бір бөлігін алып тастайды, осы кезде жаңадан таразы тепе-теңдік күйге келетін болады.
Сызықтық өлшемдерді өлшеу
Штангенциркуль, микрометр.
Қарапайым жағдайда ұзындықты өлшеу–эталонды ұзындықпен салыстыру болып табылады. Өлшеу дәлдігін арттыру мүмкін болатын қателіктердің көзін жою. Шкаламен жұмыс жасаған кезде мұндай қателіктер шкаланың біркелкі болмауынан, шкала штрихтарының қалыңдығынан болуы және т.б. Барлық алынған өлшеу құралдарын дұрыстау қателік көздерін жою және шкала бөліктерін азайтумен шектеледі.
Штангенциркуль. Штангенциркуль бөліктерге бөлінген сызғыштан, араларына өлшенетін дене орналастырылған екі қысқаштан тұрады. Қысқыштың біреуі қозғалыссыз, онымен сызғыштың нөлдік санағы байланысады, екінші қысқыш сызғыш бойымен, дене өлшемі бойында сырғиды.
Штангенциркуль
Сурет 1
Әдетте, барлық құралдар шкаласы нониуспен қамтамасыз етіледі. Бастапқыда айтылғандай шкала бойынша жіберілген қателіктер шкаланың бөліктерінің жартысына тең. Мұндай баға – адам көзі шкаланың бөліну бөлігін 0,15-0,20 бөлікке тең дәлдікпен анықтауға байланысты. Өлшенетін дененің ұштары шкала штрихтарымен сәйкес келе бермейтіндіктен, қатені қателіктер құны деп бағалау алынды. Алайда, шкаланың дәл осындай бөлікке бөлінуі кезінде өлшеу дәлдігі артуы мүмкін. Шкаланың екі штрихтарын шкала штрихтарының енінің жартысына дейінгі дәлдікпен біріктіруге болады. Егер штрихтің ені басты бөліктің 0,05 – ін құрайтын болса, онда штрихтарды басты бөліктің 0,05 шамасының дәлдігімен біріктіруге болады. Бұл үшін қозғалыстағы қысқыш қосымша шкаламен жалғанады. Бұл шкала былай құрастырылады, яғни басты шкаланың бөлінген n бөліктеріне сәйкес келетін ұзындық қосымша шкалада n – 1 немесе n +1 бөліктерге бөлінуге тиіс. Сонда, қосымша шкаланың (нониустың) бір бөлігі басты шкаланың бөліктерінен 1/n-ге айырмашылықта болады. Егер нониус бөлігі басты шкала бөлігінен кем болса, онда нониус бірінші ретті нониус немесе тура нониус деп аталады. Егер нониус бөлігі шкала бөлігінен артық болса, онда ол кері немесе екінші ретті нониус деп аталады.
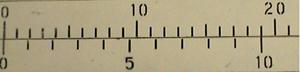
Бірінші ретті нониус
Сурет 2
Егер дене ұзындығы шкаланың бөлігінің бүтін санынан DL айырмашылықта болса, онда нониус DL-1/ n бөліктері сәйкес келеді. Бұл әдетте шкаламен салыстырғанда өлшеу дәлдігін – 20-10 есе арттыруға мүмкіндік береді.
Әр түрлі құрастырудан тұратын нониус барлық жағдайларда бұрыштық немесе сызықтық шамаларды өлшеу үшін қолданылады. Осы жағдайда олардың құрастырушысының айырмашылығы барлық нониус үшін шкала штрихының ені есебінен өлшенетін дене мен шкаланың бірігуі нәтижесінде дәлдіктің өсуі болып табылады.
Микрометр. Микрометрлік бұранда. Аз ұзындықтарды өлшегенде дәл санаумен бірге қозғалыстағы қысқыштың орын ауыстыруын ескеру қажет. Әдетте, ол микрометрлік бұранда көмегімен болады. Микрометрлік бұранда – бұл үлкен диаметрлі және аз жүрісті бұранда. Бұранданың бір айналымы қысқыштың аз жүріске тең арақашықтығына орын ауыстырады. Үлкен диаметрдің көмегімен бұранданың шеңберін үлкен бөліктерге бөледі (50-100 бөліктерге) және бұранда айналымының бөлігін оның жүріс бөлігіне ауыстырады. Бұранданың 0,5 мм жүрісі және бұранда шеңберінің 50 бөлікке бөлінуі – бұл 0,01 мм. дәлдікпен қалыңдықты өлшеуге мүмкіндік береді. Микрометрлік бұранданың шкаласы әдетте нониуспен қамтамасыз етілмейді, себебі бұранданың жүрісінің дәл келмеуі және бұранда қысқышының сапасы штрих қалыңдығына сәйкес келетін жүріс бөлігінен артық болады.
Микрометр
Сурет 3
Микрометр – микрометрлік бұрандамен байланысқан, бір жағында қозғалмайтын қысқышы, екінші жағында қозғалысты қысқышы бар қатаң металдық жалғаудан тұрады.
Микрометрмен жұмыс жасағанда, барлық өлшенетін денеге бірдей күш беру керек. Микрометрлік бұранданың ұстайтыны сол бұранданың фрикциондық берілісімен байланысқан.
№1 ЗЕРТХАНАЛЫҚ ЖҰМЫС
ЗАТТАРДЫҢ ТЫҒЫЗДЫҒЫН АНЫҚТАУ
Жұмыстың мақсаты: Дененің сызықтық өлшемдерін және массасын өлшеу кезіндегі қолданылатын басты тәсілдермен танысу, берілген заттың тығыздығын анықтау, жіберілген қателікті бағалау.
Қажетті құрал-жабдықтар: Штангенциркуль, микрометр, таразы, стакан, әр түрлі пішіндегі қатты денелер, тазартылған су, май, глицерин.
Тығыздық деп дененің массасының көлеміне қатынасын айтамыз. Жалпы жағдайда әр түрлі нүктелердегі тығыздық әр түрлі және массаның көлемге қатынасының туындысы арқылы анықталады.
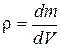
Біртекті дененің тығыздығы оның массасының көлеміне қатынасы арқылы табылады.
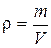
Сонымен тығыздықты анықтау үшін дененің көлемі мен массасын өлшеу керек.
Дұрыс пішінді геометриялық денелердің көлемін өлшеу – дененің сызықтық өлшемдерін – ұзындығын, ені мен биіктігін өлшеу арқылы жүзеге асады.
Жаттығу №1. Дұрыс геометриялық пішінді дененің тығыздығын анықтау
1. Микрометрді және штангенциркульді қолдану әдістерімен танысу.
2. Штангенциркульмен берілген қатты дененің қалыңдығын xi, ұзындығы yi мен енін zi 5 рет өлшеу керек.
3. Дененің m массасын анықтаңыз.
4. Стьюдент коэфициентін tр, n-1 кестесі бойынша өлшеу сандары (n-1) мен берілген сенім ықтималдылығы Р үшін табу керек.
| № п/п | уi, мм | <у>, мм | Dуi, мм | (Dуi)2 | S<у> | Ру | tp, n-1 | eу |
| № п/п | zi, мм | <z>, мм | Dzi, мм | (Dzi)2 | S<z> | Рz | tp, n-1 | ez |
| № п/п | xi, мм | <x>, мм | Dxi, мм | (Dxi)2 | S<x> | Рх | tp, n-1 | ex |
5. Берілген сенім ықтималы Р арқылы тікелей өлшеудің нәтижелерінің сенім аралықтарын есептеу керек.
6. Орташа мәндері бойынша, заттың тығыздығын <r> есептеңіздер және зат дайындалған материалдың тығыздығын анықтамалық кестеден табыңыздар.
7. Салыстармалық қателік пен сенімділік аралығын анықтаңыздар.
8.Өлшеудің соңғы нәтижесін жазыңыздар.
Жаттығу № 2 Гидростатикалық өлшеу әдісімен дене тығыздығын анықтау
Дұрыс геометриялық емес дененің сызықтық өлшемдерінен көлемді табу мүмкін емес. Бұл жағдайда Архимед заңына сүйеніп, гидростатикалық өлшеу әдісі қолданылады.
Егер ауада денені өлшеу кезінде әр түрлі салмақты кірлер массасы М болса, онда Архимед заңына сәйкес таразының тепе-теңдік шарты:
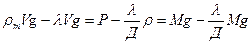
мұндағы, 
– дене тығыздығы, g – еркін түсу үдеуі, Р-ауадағы дене салмағы, V-дене көлемі, М -ауа тығыздығы, Д-әр түрлі салмақты кірлер материалының тығыздығы, l-ауа тығыздығы.
Денені суға батырғандағы тепе-теңдік шартын ұқсас етіп былай жазуға болады:
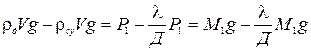
мұндағы, P1 – судағы дене салмағы, М1- суда өлшеген кездегі кірлер массасы.
Осы қатынастардан шығатыны:
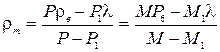
Алынған нәтиже тек қатты денелердің тығыздығын ғана анықтап қоймай, сонымен бірге қатты дененің тығыздығы белгілі болғандағы сұйықтың тығыздығын да анықтайды.
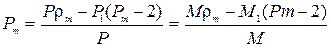
t0 C температура мен h мм. сынап бағанасы қысымындағы ауа тығыздығы былайша анықталады:
немесе абсолют температурасы Т= К және қысымы Р (Паскаль) болғандағы ауа тығыздығын l төмендегі өрнекпен анықтауға болады.
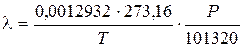
Кесте
Әр түрлі температурадағы және қалыпты атмосфералық қысымдағы судың тығыздығы
| to C | r кг/м3 | to C | r кг/м3 | to C | r кг/м3 |
| 999,841 999,900 999,941 999,965 999,973 999,965 999,941 999,902 999,849 999,781 999,700 | 999,605 999,498 999,377 999,244 999,099 998,043 998,774 998,595 998,405 998,203 | 997,922 997,770 997,538 997,296 997,044 996,783 996,512 996,232 995,944 995,646 |
Кесте
Әр түрлі температурадағы және қалыпты қысымдағы құрғақ ауаның тығыздығы
| to C | l0 кг/м3 | to C | l кг/м3 | to C | l0 кг/м3 |
| 1,293 | |||||
1. Таразы табақшасы ілгішіне жіңішке жіпті бекітіңіз де, таразыларды тепе-теңдікке келтіріңіз. Жіптерге кішкентай денелерді іліңіз де, ереже бойынша өлшеп, әр түрлі салмақты кірлердің массаларын табыңыз.
2. Осы денені стақандағы суға батып тұратындай етіп ілу керек, бірақ ол стақан қабырғасына да, оның түбіне де тимейтін болсын. Сондай-ақ, дененің үстіңгі бетінде ауа түйіршіктері болмау керек. Қайтадан таразыларды тепе-теңдікке келтіріп, әр түрлі салмақты кірлер массасын М табыңыз. Осылардың массасын біле отырып, шариктің тығыздығын табыңыз. Су тығыздығының мәнін кестеден алу керек.
3. Осы өлшеуді 5 рет қайталап, оның орташа мәні мен орташа квадраттық қатесін табыңыздар.
мұндағы r0- ауа қысымы.
Жаттығу №3 Сұйық тығыздығын анықтау
Шарикті суы бар стақаннан алыңыз да, жақсылып сүртіп құрғатыңыз. Содан кейін жіпке ілінген денені қайтадан зерттелетін сұйық ішіне батырыңыз. Дене ыдыс қабырғаларымен жанаспау керек. Сұйық бетінде ауа көпіршіктерінің болмауын қадағалаңыз. Таразыны қайтадан теңестіріп кірлер массасын М өлшеңіз. Кірлер массасын біле отырып, дене тығыздығын есептеңіз. Су тығыздығының мәнін кестеден алыңыздар.
1. Штангенциркульмен шарик диаметрін өлшеп, оның өлшенген массасын біле отырып, тығыздығын анықтау керек. Өлшеуді 5 рет қайталап, орташа мәнін табыңыз.
2. Алынған нәтижелерді салыстырыңыз.
3. Жіптегі шарикті майы немесе глицерині бар стаканға салу керек. Таразыны тепе-теңдікке келтіріп, әр түрлі салмақты кірлер массасын табыңыз. Ауада және сұйықтықта әр түрлі салмақты кірлер массасын біле отырып, сұйықтың тығыздығын табу керек. Өлшеуді 5 рет қайталаңыз.
Бақылау сұрақтары:
1. Тікелей және жанама өлшеу дегеніміз не?
2. Қандай қателік түрлері бар?
3. Нониус дегеніміз не?
4. Өлшеу дәлдігін қалай анықтаймыз?
5. Заттың тығыздығы деген не?
6. Тығыздық қандай өлшем бірлікпен өлшенеді?
7. Архимед заңын жазыңыз. Итергіш күш дегеніміз не? Кері итергіш күш түсірілетін нүкте қайда орналасқан?
№ 2 ЗЕРТХАНАЛЫҚ ЖҰМЫС
БАЛЛИСТИКАЛЫҚ МАЯТНИК КӨМЕГІМЕН ОҚТЫҢ ҰШУ ЖЫЛДАМДЫҒЫН АНЫҚТАУ
Жұмыстың мақсаты: Оқтың ұшу жылдамдығын анықтау.
Қажетті құрал-жабдықтар:ЛКМ 2-1 қондырғысы, әр түрлі оқтар, таразы.
Баллистикалық маятник ауыр дене ілінген тік созылмайтын жіптерден тұрады. Оған оқ атылған кезде, ол тік жазықтықта еркін ауытқиды.
Егер маятник пен оқтың соғылу ұзақтығы маятниктің тербеліс Т периодымен салыстырғанда кіші болса, онда маятниктің соғылу уақыты ішінде өз күйінен ауытқып үлгермейді. Бұл дегеніміз, соққы алған уақыт ішінде маятникті өз күйіне қайтып әкелетіндей күштер пайда болмайды. Сондықтан «оқ- маятник» жүйесін тұйық деп қарастыруға болады және оған қозғалыс мөлшерінің сақталу заңын және қозғалыс мөлшерінің моментін қолдануға болады. t << Т шартында
mu =(M+m)U
мұндағы M - маятник массасы, m- оқ массасы, U - соққыдан кейінгі оқ тиген маятниктің жылдамдығы.
Бұл теңдеуді біреуінде қозғалмайтын айналу осі бар екі қатты денелердің соқтығысуы туралы есептерге қолдану тиімсіз болар еді. Маятниктің өлшемі ілінген жіптер ұзындығынан кіші болғандықтан, қозғалыс мөлшерінің сақталу заңын қолдану мүмкіндігі бар, яғни маятникті математикалық деп қарастыруға болады, сонда қозғалыс мөлшері моментінің сақталу заңының теңдеуі «оқ- маятник» жүйесі үшін қозғалыс мөлшерінің сақталу заңының теңдеуіне ауысады.
Соққыдан кейін маятник көлденең ось маңайында бұрылады және оның ауырлық центрі h биіктікке көтеріледі. Соққыдан кейінгі механикалық энергияның сақталу заңы мына түрде жазылады:
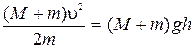
осыдан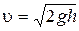 
Енді соққыға дейінгі оқ жылдамдығын табайық:
Тік орын ауыстыруды өлшеу қиын болғандықтан, оны көлденең орын ауыстырумен ауыстырып өлшеуге болады.
Сурет 10
Шындығында, 10 - суреттен көрініп тұрғандай маятниктің массалық центрінің көтерілу биіктігі h мынаған тең:
h=l-lcosa=l(1-cosa)=l*sin2a /2
сонда
кіші бұрыштар үшін: sin 
сонда
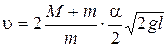
10-суреттен көрініп тұрғандай, sina=S/l . Бұрыш аз болғандықтан,
sina » a, a=S / l
және
.
M>>m болғандықтан, соңғы нәтиже мынадай болады:
Осы жұмыста қолданған тәжірибелік қондырғы - баллистикалық маятник цилиндрден тұрады. Цилиндрдің орталық бөлігі пластилинмен толтырылған. Цилиндр маятниктің көлденең ауытқуын тудырудан сақтайтын төрт жіпке ілінген, өйткені оқ цилиндрдің осінен қырына кіруі мүмкін.
Жұмыстың орындалу реті
1. Таразыда үш немесе бес оқтың массасын өлшеп, бір оқтың массасының орташа мәнін табыңыз.
2. Цилиндрге оқ атылуды жүзеге асырыңыз және көлденең ығысу S шамасын өлшеңіз. Оқтың қозғалыс троекториясы цилиндр осі арқылы өтетін тік жазықтықта жатуын тексеріңіз және оқ пластилинге тірелуі тиіс. Тәжірибені 3-5 рет қайталаңыз.
3. S-тің ығысуының орташа мәнін есептеңіз.
4. Оқтың жылдамдығын есептеңіз (М=0,287кг,ℓ =0,34м; g=9,81м/с2).
5. Кестеге берілген өлшеу мен есептеу нәтижелерін жазыңыз.
| М (кг) | ℓ (м) | mорт (м) | Sорт (мм) | S (мм) | ∆Sорт (мм) | ∆S (мм) | V (м/с) |
6. Оқтың жылдамдығын өлшеу кезіндегі абсолют және салыстырмалы қателіктерді табыңыз.
Бақылау сұрақтары
1. Оқ жылдамдығын анықтаған кезде, өлшеу қателігін қандай шама жібереді? Қателікті кеміту үшін қандай шаралар қолдану керек?
2. Энергия мен импульстің сақталу заңдарын формула түрінде жазыңыз.
3. Оқтың кинетикалық энергиясы серпімсіз соққы кезінде маятниктің потенциалдық энергиясына толығымен ауысады деп есептеуге бола ма?
4. Абсолют және салыстырмалы қателіктердің формуласын жазыңыз. Қандай шаманы өлшеу үлкен қателік жібереді? Неліктен?
5. «Маятник- оқ» жүйесін неге тұйық деп қарастыруға болады?
6. Оқ жылдамдығын динамикалық тәсілмен анықтау қандай заңдарға негізделген?
7. Қандай соққы абсолют серпімсіз деп аталады?
8. Серпімсіз соққы нәтижесінде энергияның кемуі неге тәуелді?
№ 3 ЗЕРТХАНАЛЫҚ ЖҰМЫС
ОБЕРБЕК МАЯТНИГІНІҢ КӨМЕГІМЕН ҚАТТЫ ДЕНЕНІҢ АЙНАЛМАЛЫ ҚОЗҒАЛЫСЫ ДИНАМИКАСЫНЫҢ НЕГІЗГІ ЗАҢЫН ТЕКСЕРУ
Жұмыстың мақсаты: Обербек маятнигі көмегімен қатты дененің айналмалы қозғалысының заңдылықтарымен тәжірибе арқылы танысу.
Керекті құрал – жабдықтар: Обербек қондырғысы, штангенциркуль, миллиметрлік сызғыш, электрлік секундомер, жүктер жиыны, ELWRO қондырғысы.
Обербек маятнигі қос шкивке бекітілген крестовинадан (бір-біріне 900 бекітілген екі білеу) тұрады. Оның айналыс осі горизонталь орналастырылады да, подшипниктерге бекітіледі (15-сурет). Аспаптың айналысы шкивке оралған жіп көмегімен жүзеге асырылады. Керілу күшінің
 |
 |
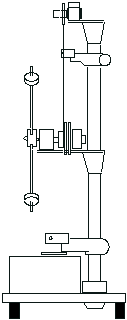Сурет 15
өзгерісі жіптің бос ұшына бекітілген әр түрлі массалы жүктер көмегімен жасалады. Құралдың инерция моментін бір пішіндегі бірдей массалы төрт жүкті стержендер бойымен қозғалту арқылы өзгертуге болады. Аспаптың айналмалы қозғалысының теңдеуін үш шама байланыстырады: жіптің керілуінің күш моменті, бұрыштық үдеу және аспаптың инерция моменті. Жіптің керілуінің күш моментін және бұрыштық үдеуді ілінген жүктің ілгерілемелі қозғалысының үдеуін біле отырып есептеуге болады. Үдеу жүктің жүріп өткен арақашықтығы мен оған сәйкес уақыт аралығымен анықталады. Сонымен қондырғының инерция моментін тәжірибеде өлшенген шамалар көмегімен есептеуге болады. Құлап келе жатқан жүк үшін:
.
Маятниктің айналатын бөлігі үшін айналмалы қозғалыс динамикасының негізгі теңдеуі:
, 
, 
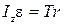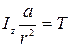Массасы М жүктің ілгерілемелі қозғалып келе жатқан жүк үшін Ньютонның екінші заңы (қозғалыс бағытындағы проекциясы):
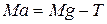
Осыдан
ал инерция моменті Іz үшін мынадай теңдеу алынады:
мұндағы, М – жіпке байланған жүк массасы;
r – шкив радиусы;
h – жүк жүріп өтетін қашықтық;
t – h биіктікті жүктің жүріп өтетін арақашықтығы;
g – еркін түсу үдеуі.
Жаттығу №1
Обербек маятнигіндегі инерция моментін және үйкеліс күші моментін анықтау, 
теңдігін тексеру.
1. Маятник білеулерінің ұштарына жүктерді бекітіңіз. Маятникті теңестіріңіз. Ол үшін алдымен бір диаметр бойында орналасатын екі жүкті бекітіп, маятникті қозғалысқа келтіріңіз. Оның қалай айналып тоқтайтынын қадағалаңыз. Маятникті дұрыс теңгерген кезде оның айналысының тежелуі бірқалыпты болуы керек, ал соңғы орналасу күйінің орны бізге бәрібір. Осыдан кейін қалған екі жүкті стержень ұштарына бекітіп, маятникті теңгеруді тағы қайталау керек. Қажет болса, жүктерді жылжытуға болады.
2. Жіптегі жүк шамасын арттыра отырып, стержендердегі жүктердің белгіленген күйі үшін бұрыштық үдеуді 7- 8 рет өлшейміз. e= f ( Мr ) тәуелділігінің графигін салыңыз. Графиктен инерция моменті мен үйкеліс күші моментін анықтаңыз. Инерция моменті графиктегі қисықтың көлбеулік бұрышының ctg-не тең, ал үйкеліс күшінің моменті – салған қисығымыздың Mr осімен қиылысу нүктесіне тең.
Жүктерді білеуден алып, крестовинаның инерция моментін I0 жүксіз анықтаңыз. Алынған нәтижені төмендегі өрнекпен салыстырыңыз:
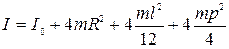
мұндағы R – крестовинадағы жүктердің массалар ортасынан айналыс осіне дейінгі қашықтық, l- крестовинадағы жүктер биіктігі, p – оның радиусы.
3. Нәтижелерді 1 – кестеге толтырыңыз.
1- кесте
| № | 
| Уақыт t(c) | Үдеу a(м/c2) | E (1/c2) | Mr (мм) | I | |
 =
| |||||||
| Жүксіз | |||||||
| l2= |
Жаттығу №2
(2) қатынасының дұрыстығын тексеру:
1. Жіпке ілінген жүк массасының тұрақты күйінде крестовинадағы жүктердің екі әр түрлі жағдайы үшін инерция моменті мен бұрыштық үдеуін өлшеңіз. қатынасының дұрыстығын тексеріңіз. Нәтижелерін 2 – кестеге толтырыңыз.
Қозғалыс теңдеуін тәжірибемен тексеруді екі түрлі жолмен жүргізуге болады:
1. Аспаптың инерция моменті өзгермеген жағдайда мына қатынас сақталуы керек:
2. Жіпке ілінген жүк массасының тұрақты болған (күш моменті тұрақты болғанда) кезінде мына қатынас орындалуы керек:
мұндағы, m – крестовинадағы жүктер массасы,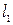 
және 
- жүктердің айналу осінен ауырлық центріне дейінгі арақашықтық.
Бақылау сұрақтары
1. Нүктемен және қозғалмайтын осьпен салыстырғандағы күш моменті деп нені атайды?
2. Дененің инерция моменті неге тәуелді, ол айналмалы қозғалыс кезінде қандай роль атқарады?
3. Құралдың жіптеріне ілінген жүктердің ілгерілемелі қозғалысында үдеу осы жұмыста қалай анықталады?
4. Тәжірибелік және теориялық жолмен алынған инерция моменті мәндерінің айырмасы қандай?
5. Бұл жұмыс қандай заңға негізделген? Осы заңды формула түрінде беріңіз.
6. Сызықты және бұрыштық үдеулер арасында қандай байланыс бар? Қандай шартта ол пайда болады?
7. Обербек маятнигін қандай күш моменті айналмалы қозғалысқа келтіреді? Осы берілген жұмыста күш моментін қалай өзгертуге болады?