Занятие 3. «Кинематика материальной точки и вращательного движения»

1. Точка движется, замедляясь, по окружности радиусом R так, что в каждый момент времени ее тангенциальное и нормальное ускорение по модулю равны друг другу. В начальный момент t = 0 скорость точки равна v₀. Найти: а) скорость точки в зависимости от времени и от пройденного пути S; б) полное ускорение точки в функции скорости и пройденного пути.

а)

Так как w_τ = w_n и точка замедляется, то:

б)

Ответ: а) ; ; б) .

2. Твёрдое тело вращается вокруг неподвижной оси по закону φ = at – bt³, где a = 6 рад/с, b = 2 рад/с³. Найти: а) средние значения угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки; б) угловое ускорение в момент остановки тела.

а)

б)

Ответ: а) ; ; б) .

3. Точка движется по плоскости так, что её тангенциальное ускорение w_τ = a, а нормальное w_n = bt², где a и b – положительные постоянные, t – время. В момент t = 0 точка покоилась. Найти зависимости от пройденного пути S радиуса кривизны R траектории точки и её полного ускорения w.

Ответ: ; .

4. Твёрдое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота по закону ω = ω₀ – aφ, где ω₀и a – положительные постоянные. В момент времени t = 0 угол φ = 0. Найти зависимости от времени: а) угла поворота; б) угловой скорости.

а)

При t = 0 и φ = 0:

б)

Ответ: а) ; б) .

5. Частица движется по дуге окружности радиуса R по закону l = A sin ωt, где l – смещение из начального положения, A и ω постоянные. Найти полное ускорение частиц в точках l = 0 и l = ±A.

Если l = 0:

Если l = ±A: ;

Ответ: ; .

6. Колесо вращается вокруг неподвижной оси так, что угол φ его поворота зависит от времени как φ = at², где a = 0,2 рад/с². Найти полное ускорение w точки A на ободе колеса в момент времени t = 2,5 с, если линейная скорость A в этот момент v = 0,65 м/с.

Ответ: .

7. В момент t = 0 частица вышла из начала координат в положительном направлении оси x. Её скорость меняется со временем по закону , где - вектор начальной скорости, модуль которого v₀ = 10 см/с, τ = 5,0 с. Найти: а) координату x частицы в момент времени 6, 10 и 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10 см от начала координат; в) путь S, пройденный частицей за первые 4 и 8 с.

а)

б) При S = 10 см:

При S = -10 см: ;

– время не может быть отрицательным;

в) При t < τ: ;

При t = τ: ;

При t > τ:

При t = 4 с:

При t = 8 с:

Ответ: а) ; ; ; б) ; ; ; в) ; .

8. Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от её скорости v по закону , где a – положительная постоянная. В начальный момент скорость точки равна v₀. Какой путь она пройдёт до остановки? За какое время этот путь будет пройден?

При v = 0:

Ответ: ; .

9. Радиус-вектор частицы меняется со временем t по закону , где - положительный вектор, α – положительная постоянная. Найти: а) скорость 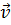и ускорение 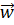частицы в зависимости от времени; б) промежуток времени Δt, по истечении которого частица вернётся в исходную точку, а также путь S, который она пройдёт при этом.

а)

б)

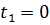
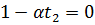
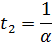
Ответ: а) ; ; б) ; .