ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
ЛАБОРАТОРНАЯ РАБОТА №5
Тема:Решение задач с использованием средства MS Excel подбор параметра.
Цель работы: научиться решать задачи с использованием средства MS Excel подбор параметра.
Содержание работы:
1) выполнить задание согласно вашему варианту;
2) оформить отчет, включающий: лист задания, вариант индивидуального задания, результаты, вывод. Требования к оформлению отчета:
- параметры страницы: левое – 3, правое – 1,5, верхнее – 1,5, нижнее – 2;
- шрифт - Times New Roman, размер – 14 пт;
- выравнивание по ширине, красная строка отступ – 0,7;
- заголовки отделены от текста двумя пустыми строками.
ТСО:
- текстовый редактор Word;
- табличный редактор Excel.
Объем работы: 2 часа.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
Вариант 1
Используя средство Excel – Подбор параметра решите следующую задачу:
Сколько необходимо дней, чтобы сумма выплаты составляла 500 000 р.? Если цена одной акции – 15000, акций было куплено – 10, процентная ставка 5%, проценты пересчитываются каждый день.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в день)количество дней;
· Для расчета суммы выплаты используется следующая формула: =стоимость акций* коэффициент наращивания* количество акций.
Вариант 2
Используя средство Excel – Подбор параметра решите следующую задачу:
Какую сумму необходимо положить в банк, чтобы через пять лет сумма выплаты составляла 100 000 р.? Если процентная ставка 12%, проценты пересчитываются каждый год.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в год)количество лет;
· Для расчета суммы выплаты используется следующая формула: =сумма вклада* коэффициент наращивания.
Вариант 3
Используя средство Excel – Подбор параметра решите следующую задачу:
Сколько необходимо купить акций, чтобы в течении 30 дней сумма выплаты составила 1000 000 р.? Если цена одной акции – 30000, процентная ставка 8%, проценты пересчитываются каждый день.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в день)количество дней;
· Для расчета суммы выплаты используется следующая формула: =стоимость акций* коэффициент наращивания* количество акций.
Вариант 4
Используя средство Excel – Подбор параметра решите следующую задачу:
Под какой процент необходимо положить 45000 р. в банк, чтобы через три года сумма выплаты составляла 80 000р.? Если проценты пересчитываются каждый год.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в год)количество лет;
· Для расчета суммы выплаты используется следующая формула: =сумма вклада* коэффициент наращивания.
Вариант 5
Используя средство Excel – Подбор параметра решите следующую задачу:
Какой должна быть процентная ставка, чтобы в течении 20 дней сумма выплаты составляла 70 000 р.? Если цена одной акции – 5000, акций было куплено – 4, проценты пересчитываются каждый день.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в день)количество дней;
· Для расчета суммы выплаты используется следующая формула: =стоимость акций* коэффициент наращивания* количество акций.
Вариант 6
Используя средство Excel – Подбор параметра решите следующую задачу:
Сколько необходимо лет, чтобы сумма выплаты составляла 500 000 р.? Если сумма вклада 49000р., процентная ставка 15%, проценты пересчитываются каждый год.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в год)количество лет;
· Для расчета суммы выплаты используется следующая формула: =сумма вклада* коэффициент наращивания.
Вариант7
Используя средство Excel – Подбор параметра решите следующую задачу:
Сколько необходимо дней, чтобы сумма выплаты составляла 700 000 р.? Если цена одной акции – 13000, акций было куплено – 14, процентная ставка 7%, проценты пересчитываются каждый день.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в день)количество дней;
· Для расчета суммы выплаты используется следующая формула: =стоимость акций* коэффициент наращивания* количество акций.
Вариант 8
Используя средство Excel – Подбор параметра решите следующую задачу:
Какую сумму необходимо положить в банк, чтобы через семь лет сумма выплаты составляла 110 000 р.? Если процентная ставка 14%, проценты пересчитываются каждый год.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в год)количество лет;
· Для расчета суммы выплаты используется следующая формула: =сумма вклада* коэффициент наращивания.
Вариант 9
Используя средство Excel – Подбор параметра решите следующую задачу:
Сколько необходимо купить акций, чтобы в течении 29 дней сумма выплаты составила 700 000 р.? Если цена одной акции – 12000, процентная ставка 11%, проценты пересчитываются каждый день.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в день)количество дней;
· Для расчета суммы выплаты используется следующая формула: =стоимость акций* коэффициент наращивания* количество акций.
Вариант 10
Используя средство Excel – Подбор параметра решите следующую задачу:
Под какой процент необходимо положить 53000 р. в банк, чтобы через четыре года сумма выплаты составляла 130 000р.? Если проценты пересчитываются каждый год.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в год)количество лет;
· Для расчета суммы выплаты используется следующая формула: =сумма вклада* коэффициент наращивания.
Вариант 11
Используя средство Excel – Подбор параметра решите следующую задачу:
Какой должна быть процентная ставка, чтобы в течении 26 дней сумма выплаты составляла 88 000 р.? Если цена одной акции – 9000, акций было куплено – 6, проценты пересчитываются каждый день.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в день)количество дней;
· Для расчета суммы выплаты используется следующая формула: =стоимость акций* коэффициент наращивания* количество акций.
Вариант 12
Используя средство Excel – Подбор параметра решите следующую задачу:
Сколько необходимо лет, чтобы сумма выплаты составляла 630 000 р.? Если сумма вклада 37000р., процентная ставка 14%, проценты пересчитываются каждый год.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в год)количество лет;
· Для расчета суммы выплаты используется следующая формула: =сумма вклада* коэффициент наращивания.
Вариант 13
Используя средство Excel – Подбор параметра решите следующую задачу:
Сколько необходимо дней, чтобы сумма выплаты составляла 660 000 р.? Если цена одной акции – 17600, акций было куплено – 12, процентная ставка 7%, проценты пересчитываются каждый день.
· Коэффициент наращивания рассчитывается по формуле: =(1+процентная ставка в день)количество дней;
· Для расчета суммы выплаты используется следующая формула: =стоимость акций* коэффициент наращивания* количество акций.
Теоретический материал
1 ПОДБОР ПАРАМЕТРА
При обработке табличных данных часто возникает необходимость в прогнозировании результата на основе известных исходных значений или, наоборот, в определении того, какими должны быть исходные значения, позволяющие получить нужный результат.
Использование средства подбора параметра
Рассмотрим, как работает средство подбора параметра, позволяющее определить исходное значение, которое обеспечивает заданный результат функции. В качестве примера возьмем таблицу, с помощью которой рассчитывается размер пенсионных накоплений (рис. 1).

Рисунок 1 – Таблица для расчета размера пенсионных накоплений
В этой таблице указаны возраст, начиная с которого в пенсионный фонд вносятся платежи (А2), величина ежемесячного взноса (В2), период отчислений, рассчитанный по формуле:
=60-A2
Мы предполагаем, что речь идет о мужчине, который выйдет на пенсию в 60 лет (С2), а также величина процентной ставки составляет 12% (D2).
Сумма накоплений рассчитывается с помощью функции по следующей формуле:
=БС(D2;C2;-B2*12;;1)
Функция БС() возвращает будущее значение вклада, определяемое с учетом периодических постоянных платежей и постоянной процентной ставки. Синтаксис данной функции выглядит так:
БС(ставка;кпер;плата;нз:тип)
Перечислим ее аргументы: ставка - размер процентной ставки за период; кпер - общее число периодов выплат годовой ренты; плата - выплата, производимая в каждый период (это значение не может меняться на протяжении всего времени выплат), причем обычно плата состоит из основного платежа и платежа по процентам; нз - текущая стоимость или общая сумма всех будущих платежей, начиная с настоящего момента (по умолчанию - 0); тип - число, которое определяет, когда должна производиться выплата (0 - в конце периода, задается по умолчанию, 1 - в начале периода).
Формула имеет такой вид, так как мы предполагаем, что проценты начисляются не ежемесячно, а в начале, следующего года за предыдущий год.
Ежемесячная прибавка к пенсии рассчитывается по следующий формуле:
=Е2*D2/12
Допустим, нам необходимо определить, в каком возрасте будущему пенсионеру надо начинать выплаты, чтобы потом получить прибавку к пенсии в размере 1000 руб. Для этого следует выделить ячейку, отведенную для представления результата (в нашем случае F2), и вызвать команду Сервис/Подбор параметра. Когда появится диалоговое окно Подбор параметра(рис. 2), адрес выделенной ячейки будет автоматически вставлен в поле Установить в ячейке. Укажите в поле Значение целевое значение - 1000. Поместите курсор ввода в поле Изменяя значение ячейки и выделите ячейку А2, после чего ее адрес отобразится в указанном поле.

Рисунок 2 - Диалоговое окно Подбор параметра с заданными параметрами
При использовании функции подбора параметра необходимо, чтобы ячейка с целевым значением содержала ссылку на ячейку с изменяемым значением.
После выполнения всех установок нажмите кнопку ОК, и поиск нужного значения будет начат. Результат вычисления отобразится в диалоговом окне Результат подбора параметра, а также в исходной таблице (рис. 3). После нажатия кнопки ОК полученные значения будут вставлены в таблицу.
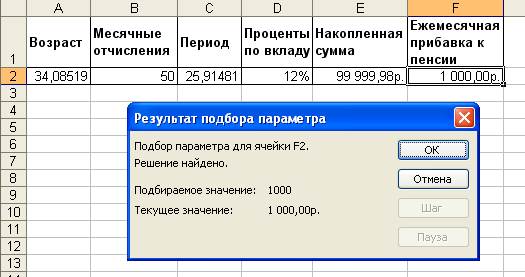
Рисунок 3 - Результаты подбора параметра
Результат работы сохраните на Лист 1.
Скопируйте таблицу для расчета размера пенсионных накоплений на Лист 2 и путем подбора параметра определите, какими должны быть ежемесячные отчисления, чтобы за 10 лет получить прибавку к пенсии в размере 3000 руб. Результат работы сохраните на Лист 2.