Анализ ряда распределения регионов по численности населения на 1 января 2013 года (млн. чел)

Распределение регионов по численности населения на 1 января 2013 года (млн. чел)

Таблица 2.4

Численность населения	колличество регионов	Середины ин-тервалов, хi	Накопленные частоты S	xi fi	Ixi - I2 fi
0.21 - 0.89		0,55		3,3	10,91
0.89 - 1.58		1,23		11,07	4,024
1.58 - 2.26		1,92		5,76	0,0013
2.26 - 2.95		2,6		18,2	3,44
2.95 - 3.63		3,29		13,16	7,74
3.63 - 4.32		5,47		5,47	12,75
итого				56,96	38,87

 

Среднее арифметическое значение признака:

=38,87/ 30 = 1,29

Вывод: средняя численность населения в регионах на 1 января 2013 года 1,29 млн. человек.

Мода:

+ , где

–начало интервала, содержащего моду,

-величина интервала, содержащего моду,

-частота того интервала, в котором расположена мода,

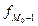–частота интервала, предшествующего модальному,

–частота интервала, следующего за модальным.

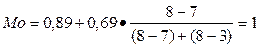
Вывод: в большинстве регионов численность населения составляет 1 млн. человек.

Медиана:

Численное значение медианы определяется по ряду накопленных частот.

, где

– начало интервала, содержащего медиану,

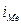– величина интервала, содержащего медиану,

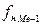– накопленная частота интервала, который стоит перед медианным,

– объем совокупности,

– частота того интервала, в котором расположена медиана.

Вывод: в половине регионов численность населения более 1,98 млн. человек, в другой половине менее 1,98 млн. человек.

Квартили.

Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q₁; 25% будут заключены между Q₁ и Q₂; 25% - между Q₂ и Q₃; остальные 25% превосходят Q₃.

 

Таким образом, 25% единиц совокупности будут меньше по величине 6,46. Q2 совпадает с медианой, Q2 = 1,98.

 

Таким образом, 50% единиц совокупности будут меньше по величине 4,47

Вывод: В четверти регионов численность населения составляет менее 6,46 млн. чел. и у четверти более 4,47 млн. человек.

 

Среднеквадратическое отклонение:

Для того чтобы посчитать среднее квадратичное отклонение, сначала необходимо найти дисперсию по формуле:

=20,23/ 30=0,67

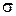= =0,81

Вывод: возможное отклонение численности населения регионов составляет 0,81

Коэффициент вариации:

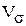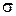= / *100% =0,81/1,87* 100%=43,31%

Вывод: совокупность не однородна, так как коэффициент вариации более 33%