Закон взаимодействия элементов тока (закон Лапласа-Био-Савара-Ампера). Полевая трактовка закона взаимодействия элементов тока. Релятивистская природа магнитного поля.

 

Эксперименты Х.Эрстеда и А.Ампера в 1820г. показали, что магнитная стрелка возле провода поворачивается при пропускании тока по проводу, и два провода с током притягиваются или отталкиваются в зависимости от направления токов в них.

Формулу для расчета силы взаимодействия удалось получить только для элементов линейного тока в 1844 г.

РИС.68

 

- закон Био-Савара-Лапласа-Ампера (формула Грассмана). Гн/м

- сила, с которой элемент тока первого контура действует на элемент тока второго контура . Если элементы токов лежат в плоскости рис. 68, то направление этой силы совпадает с направлением нормали .

Закон Био-Савара-Лапласа–Ампера экспериментально проверить нельзя, но следствия из него подтверждаются на практике.

Во всех точках пространства, окружающего произвольный ток, всегда существует обусловленное этим током поле сил, которое по сложившейся исторически терминологии называется магнитным полем.

По аналогии с электростатикой можно ввести силовую характеристику точки магнитного поля – вектор магнитной индукции:

- закон Био-Савара-Лапласа для расчета индукции магнитного поля, создаваемого элементом тока в некоторой точке. Экспериментально проверить эту формулу нельзя, но можно рассчитать индукцию магнитного поля, созданного всем контуром с током, используя установленный на опыте принцип суперпозиции магнитных полей: . -лишь формальная запись, на практике интегрирование возможно лишь для проекций вектора магнитной индукции.

Тл (Тесла).

Если задана объемная плотность тока,

то: . Тогда .

РИС.70

Магнитное поле порождается движущимися зарядами (токами). Если скорость направленного движения зарядов в проводнике , то . Тогда:

Индукцию магнитного поля точечного заряда, движущегося с постоянной нерелятивистской скоростью (рис.70) можно определить по формуле:

В_земли~5*10^-5Тл, В_мозга~10^-11Тл.

В_max ~150 Тл - получена в виде импульса.

 

из опыта (закон Кулона) непосредственно следует, что напряженность поля неподвижного точечного заряда q на расстоянии r от него можно представить как

(5)

где k — постоянная вид, которой зависит от выбора системы отсчета, в системе СИ 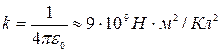; ε₀ — электрическая постоянная; — радиус-вектор, проведенный из центра поля, в котором расположен заряд q, до интересующей нас точки. Напряженность поля в системе СИ выражается в вольтах на метр (В/м). В зависимости от знака заряда q вектор направлен так же, как и (для положительного заряда), или противоположно ему (для отрицательного заряда).

Рис. 4

 

 

По существу, формула выражает не что иное, как закон Кулона, но в «полевой» форме. Вся совокупность экспериментальных фактов показывает, что этот закон справедлив для расстояний от 10 см до нескольких километров, и пока нет никаких оснований ожидать, что этот закон не выполняется и при больших расстояниях.

Принцип суперпозиции

Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:

, (6)