Закон Кулона. Экспериментальные проверки закона Кулона. Теорема Остроградского-Гаусса. Дифференциальная формулировка закона Кулона.

Закон Кулона. Кулон – 1785 – сила взаимодействия – закон:

Точечные заряды q₁ и q₂, помещенные в однородную изотропную среду, взаимодействуют друг с другом с силой

(2)

где k - постоянная вид, которой зависит от выбора системы отсчета, в системе СИ 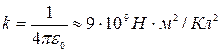(k = 1 Гауссова система); ε₀ — электрическая постоянная; ε — относительная диэлектрическая проницаемость вещества (e ³ 1, e_воды = 81).

Справедливость закона Кулона предполагает следующие допущения:

- только точечные заряды (Точечный заряд – физическая модель заряженного тела, размеры которого весьма малы по сравнению с расстоянием до других зарядов)

- изотропность среды (свойства среды в окрестностях любой точки одинаковы по всем направлениям)

- однородность среды

- безграничность среды

Кулон исследовал угол закручивания нити от силы (работал в области механики). Используя свой прибор, изображенный на рисунке

Прибор – крутильные весы, состоит из: стеклянного коромысла, серебряной нити 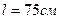, , шарика (шарик заряжают стеклянной палочкой), неподвижного шарика (его тоже заряжают).

Шарики отталкиваются, нить закручивается на угол j. Кулон установил, что сила притяжения (отталкивания) шаров пропорциональна произведению зарядов шаров и обратно пропорциональна квадрату расстояния между ними:

;

Теорема Гаусса.

Вычисление электрического поля в некоторых случая, обладающих специальной симметрией, упрощается применением теоремы Остроградского – Гаусса.

Электростатическая теор. Гаусса устан. матем. связь между потоком вектора напряженности E сквозь замкнутую поверхность S и зарядом, находящимся в объеме, ограниченной этой поверхностью.

(стационарн.)

Рис. 7

а) элементарный поток вектора через ориентиров. плоскую элементарную площадку dS ( ) есть скалярная физ. величина, равная скалярному произведению на (Рис. 7):

(9)

где Е_п— проекция вектора на нормаль к площадке . Выбор направления вектора (а следовательно, и ) условен, его можно было направить и в противоположную сторону.

Замечание:

Площадка элементарная, т.е. в пределах нее вектор постоянен.

б) Рассмотрим поверхность S. Разобьем ее на элементарные площадки dS в пределах которых вектор . Поток вект. поля напр. через поверхн. S есть сумма элементарных потоков по всем элементарным площадкам dS из которых состоит поверхность S

(10)

Эта величина алгебраическая. Она зависит не только от конфигурации поля E, но и от выбора нормали поверхн.

Замечание: Если поверхн. S – замкн, то этот факт изображ ® , а нормаль и к поверх. берется внешняя (наружу области, охватываемой поверхностью)

. Теорема Гаусса в дифференциальной форме.

Она устанавливает связь между объемной плотностью заряда r и изменениями напряженности поля в окрестности данной точки пространства.

Введем дифференц. скалярную характеристику для данной точки векторного поля – дивергенция поля (div ).

Из математики – теорема Остроградского

Þ т. Гаусса

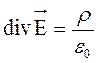
- Т.Г в дифференц. форме или дифференц. формулировка закона Кулона.

Замечание 1:

Выражение для дивергенции зависит от выбора системы координат

- декарт:

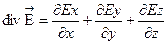
- цилиндр: .

Замечание 2:

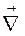Написание формулы упрощается, если ввести векторный дифф. оператор (набла), приобретающий смысл в сочетании со скалярной или векторной функцией

= ×

декарт Þ .

Замечание 3:

В тех точках поля, где div >0 имеются источники поля (полож. заряды), а где div <0 имеются стоки поля (отр. Зар.). Линии выходят из источников и заканчиваются в стоках.