Алгоритм решения задач симплекс – методом

 

Для определенности считаем, что решается задача на отыскание минимума.

1. Задачу линейного программирования привести к каноническому виду.

После введения добавочных переменных систему уравнений и линейную функцию записываем в виде, который называется расширенной системой:

 

Предполагаем, что все добавочные переменные имеют тот же знак, что и свободные члены; в противном случае используем так называемый М – метод, который будет рассмотрен ниже.

2. Определить базисные и свободные переменные.

3. Исходную расширенную систему заносим в первую симплекс – таблицу. Последняя строка таблицы, в которой приведено уравнение для линейной функции цели, называется оценочной. В ней указываются коэффициенты функции цели . В левом столбце таблицы записываем основные переменные (базис), в последующих – коэффициенты при свободных переменных. В предпоследнем столбце – свободные члены расширенной системы . Последний столбец подготовлен для оценочных отношений, необходимых для определения базисной переменной на основании соотношения (6.29).

4. Определить возможность решения задачи по значениям согласно теоремам 6.7,…, 6.9.

5. Выбрать разрешающий (опорный) элемент . Если критерий оптимальности не выполнен (не выполнены условия теоремы 6.7 или 6.8), то наибольший по модулю отрицательный коэффициент в последней строке определяет разрешающий (опорный) столбец .

Составляем оценочные отношения каждой строки по следующим правилам:

1⁰) , если все и имеют разные знаки;

2⁰) , если все и ;

3⁰) , если ;

4⁰) 0, если и ;

5⁰) , если и имеют одинаковые знаки.

Определим . Если конечного минимума нет, то задача не имеет конечного оптимума ( ). Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разрешающей (опорной) строкой. На пересечении разрешающих строки и столбца находится разрешающий (опорный) элемент .

6⁰) Переход к следующей таблице по правилам:

а) в левом столбце записываем новый базис: вместо основной переменной – переменную , т.е. поменяем местами переменные и ;

б) на место опорного элемента поставить 1;

в) на остальных местах опорной строки в новой таблице оставить элементы исходной таблицы;

г) на остальные места в опорном столбце поставить соответствующие элементы исходной таблицы, умноженные на –1;

д) на оставшиеся свободные места элементов , , 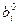в новой таблице записать числа , , , которые находятся следующим образом:

, , .

 

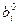Для упрощения вычислений по этим формулам их можно сформулировать в виде «правила прямоугольника» (рис. 6.8): элементы на диагоналях прямоугольника с вершинами (или , , , , или , , , ) перемножаются (произведение, не содержащее опорного элемента , берется со знаком минус) и полученные произведения складываются;

е) все полученные элементы новой таблицы разделить на опорный элемент .

7⁰) По значению элемента определить, найдено ли оптимальное значение целевой функции. В случае отрицательного ответа продолжить решение (возврат к пункту 6).

 

 

 

Рис. 6.8. Правило прямоугольника для определения чисел:

а − , б − , в − .

 

Рассмотрен алгоритм преобразования симплекс – таблиц для невырожденных допустимых базисных решений, т.е. выполнялась ситуация, описанная теоремой 6.9. Если исходная задача линейного программирования является вырожденной, то в ходе ее решения симплекс – методом могут появиться и вырожденные базисные решения. При этом возможны холостые шаги симплекс – метода, т.е. итерации, на которых f(x) не изменяется. Возможно так же и зацикливание, т.е. бесконечная последовательность холостых шагов. Для его предотвращения разработаны специальные алгоритмы – антициклины. Однако в подавляющем большинстве случаев холостые шаги сменяются шагами с убыванием целевой функции и процесс решения завершается в результате конечного числа итераций.

Пример 6.8. Решить задачу, приведенную в примере 6.7, симплекс методом.