Описание симплекс-метода
Из анализа коэффициентов в условиях задачи (6.23)…(6.25) (или в соответствующей симплекс-таблице) можно сделать одно из следующих трех утверждений:
Теорема 6.7. Если в выражении (6.23) все коэффициенты 
, то в угловой точке (6.21) достигается минимум целевой функции 
на допустимом множестве X и этот минимум равен 
.
При любом 
значение с учетом (6.23) может лишь увеличиваться по сравнению с .
Теорема 6.8. Если среди отрицательных коэффициентов 
, в (6.23) есть такой, например, 
, что в (6.24) все коэффициенты 
, то минимум целевой функции на допустимом множестве X не достигается, т.е. задача (6.23)…(6.25) не имеет решений.
Положим значения всех свободных переменных, кроме 
, равными нулю. Тогда из уравнений (6.24) получаем решение
, (6.27)
где 
. (6.28)
Оно является допустимым, поскольку все 
. При этом с учетом (6.23) 
.
Поэтому, так как 
, целевая функция неограниченно убывает с ростом 
, т.е. целевая функция не ограничена снизу, а, следовательно, не имеет решения.
Замечание. Ситуация, описанная в теореме 6.8 возможна, если допустимое множество X задачи не ограничено.
Теорема 6.9. Пусть 
является невырожденным допустимым базисным решением задачи (6.23)…(6.25), т.е. 
Тогда, если хотя бы один из коэффициентов в (6.23), например, , отрицателен ( ) и при этом среди коэффициентов 
есть хотя бы один положительный, то существует допустимое базисное решение 
множества Е, для которого 
.
Положив в (6.24) значения всех свободных переменных, кроме , равными нулю, получим решение (6.27), (6.28) системы уравнений (6.24). По условию теоремы среди коэффициентов есть положительные, поэтому с увеличением 
может произойти нарушение условий неотрицательности (6.25) для соответствующих переменных 
из выражений (6.28). Найдем ту из них ( 
), которая раньше всех обратиться в нуль при возрастании 
. С учетом (6.28) номер q находится из условия
(6.29)
где минимум берется по всем номерам 
, для которых 
.
Полагая в (6.27), (6.28) равным 
, получаем решение
(6.30)
где 
. (6.31)
Очевидно, что х1 является допустимым базисным решением системы (6.24); оно соответствует базисным переменным 
. Отметим, что в этом решении переменные хq и хk поменялись ролями: хq из базисных переменных перешла в свободные, а хk – наоборот.
Значение целевой функции (6.23) в точке x1 из (6.30) равно
.
По условию 
и, следовательно, 
.
Результаты теорем 6.7 … 6.9 лежат в основе симплекс-метода решения задач линейного программирования. Идея этого метода состоит в следующем.
Если в точке x0 из (6.21) выполняются условия теоремы 6.7 или 6.8, то решение задачи (6.16)…(6.18) на этом завершается.
Если же для точки x0 выполнены условия теоремы 6.9, то совершается переход от x0 к новому допустимому базисному решению x1 из (6.30), для которого f(x) уменьшается. Затем в точке x1 анализ коэффициентов задачи повторяется, и на основании теорем 6.7…6.9 делается одно из трех возможных заключений и т.д.
Так как число допустимых базисных решений задачи (6.16)…(6.18) не превосходит 
, то случай, описанный в теореме 6.9, может повторяться лишь конечное число раз. Поэтому в результате конечного числа шагов перехода к новому допустимому базисному решению задача будет решена или будет установлена ее неразрешимость.
Таким образом, симплекс – метод представляет собой направленный перебор допустимых базисных решений (угловых точек допустимого множества) задачи линейного программирования с последовательным уменьшением целевой функции.
Найдем канонический вид задачи, соответствующий допустимому базисному решению x1 из (6.30). Считая свободными переменные 
, т.е. поменяв местами свободную переменную 
с базисной переменной 
найдем решение системы (6.19).
Разделив q - е уравнение из системы (6.24) на 
, запишем его в виде:
. (6.32)
Выразим из равенства (6.32) переменную 
и подставим найденные выражения в остальные уравнения системы (6.24) и в формулу (6.23) для целевой функции. В результате получим:
i=1:m, i ≠ q. (6.33)
Зависимость целевой функции от новых свободных переменных примет вид:
. (6.34)
Задача линейного программирования (6.32) … (6.34) имеет канонический вид, соответствующий допустимому базисному решению x1 из (6.30)…(6.31) и может быть записана с помощью симплекс – таблицы. Компоненты нового базисного решения x1 можно найти, приравняв нулю свободные переменные 
и хq и найдя при этом условии значения базисных переменных из (6.32), (6.33).
По знакам коэффициентов в системе (6.32), (6.33) и в выражении для целевой функции (6.34) можно сделать одно из трех приведенных выше заключений, как это было сделано для угловой точки 
. В случае теоремы 6.9 следует совершить переход к очередной угловой точке 
, аналогичной переходу от x0 к x1, и т.д.
Как указано выше реализация симплекс – метода значительно упрощается при использовании симплекс - таблиц. Записав коэффициенты уравнений (6.19) и целевой функции (6.22) соответствующим образом (см. табл. 6.5), получим симплекс – таблицу задачи для угловой точки из (6.21). Здесь введен для коэффициентов 
и 
индекс 0, показывающий, что они относятся к начальной угловой точке .
Рассмотрим переход от симплекс-таблицы, соответствующей угловой точке x0 (табл. 6.5), к симплекс-таблице для угловой точки x1.
Пусть номера q и k определены так, как это сделано выше. Элемент 
, а также строка и столбец табл. 6.5, на пересечении которых он стоит, называются разрешающими или опорными.
Из формул (6.23) и (6.24) следует, что преобразование начальной симплекс-таблицы с опорным элементом 
(см. табл. 6.5) приводит к новой симплекс-таблице (табл. 6.6), для определения элементов которой необходимо выполнить операции, указанные в нижеприведенном алгоритме.
Таблица 6.5
Начальная симплекс-таблица
| Базис | Переменные | Свободный член |
| xm+1 … xk … xn | ||
| x1 . . . xi . . . xm |  …  … 
.
.
.
 …  … 
.
.
.
 …  … 
| 
.
.
.
.
.
.
|
|
|  …  … 
| 
|
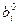Таблица 6.6
Симплекс-таблица для угловой точки x1
| Базис | Переменные | Свободный член |
| xm+1 … xq … xn | ||
| x1 . . . xk . . . xm |  …  … 
.
.
.
 …  … 
.
.
 …  … 
|
.
.
.
.
.
.
|
|
|  …  … 
| 
|
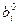