Геометрическая интерпретация двойственных задач

Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию задачи линейного программирования, можно легко найти решение данной пары задач. При этом имеет место один из следующих трехвзаимноисключающих друг друга случаев:

1) обе задачи имеют планы;

2) планы имеет только одна задача;

3) для каждой задачи двойственной пары множество планов пусто.

 

Пример 6.6. Найти решение двойственной пары задач:

· исходная задача:

f(x) = -2x₁ - 3x₂ ® min,

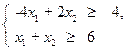
x₁, x₂ ³ 0;

· двойственная задача:

 

f(y) = 4y₁+6y₂ ® max,

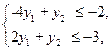
y₁, y₂ ³ 0.

 

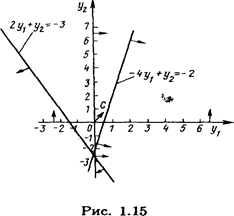
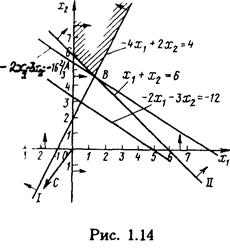
Решение. Как исходная, так и двойственная задача содержат по две переменные. Поэтому их решение находим, используя геометрическую интерпретацию задачи линейного программирования (рис. 6.5 и 6.6). Из рис. 6.5. видно, что исходная задача не имеет оптимального плана из-за неограниченности снизу ее целевой функции на множестве допустимых решений.

Рис. 6.6. Пустое многоугольное множество

Рис. 6.5. Неограниченное многоугольное множество

Из рис. 6.6. следует, что двойственная задача не имеет планов, поскольку многоугольник решений ее пуст. Это означает, что если исходная задача двойственной пары не имеет оптимального плана из-за неограниченности на множестве допустимых решений ее целевой функции, то двойственная задача не

имеет планов.