Двойственность в линейном программировании
Каждой задаче ЛП можно поставить в соответствие другую задачу ЛП, называемую двойственной. Их совместное изучение составляет предмет теории двойственности, являющейся важным разделом линейного программирования. Более эффектной теория двойственности является в тех случаях, когда двойственная задача решается проще, чем прямая.
Для удобства выпишем еще раз общую задачу ЛП:
f(x)= 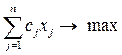 ,
,
 аij xj £ bi , i = 1:k,
аij xj £ bi , i = 1:k,
 аijxj = bi , i = (k+1):m, (6.11)
аijxj = bi , i = (k+1):m, (6.11)
xj ³ 0, j = 1: l.
Двойственной к задаче (6.11) называется следующая задача:
 ,
,
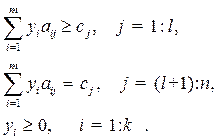 (6.12)
(6.12)
При этом задача (6.11) называется прямой.
Переход к двойственной задаче удобно осуществлять с помощью табл. 6.1.
Таблица 6.1.
Таблица перехода к двойственной задаче
х1≥0 … хl≥0 хl+1 … хn
| y1≥0 . . . yk≥0 yk+1 . . . ym | а11 … а1s а1,s+1 … а1n аk1 … аkl аk,l+1 … аkn аk+1, 1 … аk+1,l аk+1,l+1 аk+1,n . . . am1 … aml am,l+1 … amn | ≤ ≤ = = | b1 . . . bk bk+1 . . . bm |
| ≥ … ≥ = … = | |||
| с1 … cl cl+1 … cn |
Для построения двойственной задачи необходимо пользоваться следующими правилами:
1) если прямая задача решается на максимум, то двойственная – на минимум, и наоборот;
2) в задаче на максимум ограничения – неравенства имеют смысл ≤, а в задаче минимизации – смысл ≥;
3) каждому ограничению прямой задачи соответствует переменная двойственной задачи, и наоборот, каждому ограничению двойственной задачи соответствует переменная прямой задачи;
4) матрица системы ограничений двойственной задачи получается из матрицы системы ограничений исходной задачи транспонированием;
5) свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи, и наоборот;
6) если на переменную прямой задачи наложено условие не отрицательности (≥), то соответствующее ограничение двойственной задачи записывается как ограничение – неравенство, если же нет, то, как ограничение равенство;
7) 7) если i-e ограничение исходной задачи является неравенством, то i –я переменная двойственной задачи yi ³ 0. Если же i-е ограничение есть уравнение, то переменная yi может принимать как положительные, так и отрицательные значения, т.е. условие неотрицательности не налагается.
Сначала в таблицу заносится вся информация о прямой задаче: значения параметров aij, bi, и сj, знаки неравенств или равенств в ограничениях (справа), условия неотрицательности соответствующих переменных (сверху). Затем каждой i-й строке (i-му ограничению прямой задачи) ставится в соответствие двойственная переменнаяyi, на которую накладывается условие неотрицательности, если справа в этой строке стоит знак неравенства. Внизу проставляются знаки неравенства или равенства в зависимости от того, наложено или не наложено условие неотрицательности на соответствующую переменную прямой задачи. После этого двойственная задача «считывается» путем умножения вектора у= (yi) на столбцы матрицы А = (аij) и вектор b = (bi).
В табл. 6.2 указаны прямая и двойственная задачи в наиболее важных частных случаях.
Таблица 6.2
Формы записи прямой и двойственной задач
| Форма записи прямой задачи ЛП | Форма записи соответствующей двойственной задачи ЛП |
Основная: <c,x> 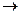 max,
Ax ≤ b, x≥ 0 max,
Ax ≤ b, x≥ 0
| Каноническая: : <b,y> 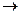 min,
yA= c, y ≥0 min,
yA= c, y ≥0
|
Стандартная: <c,x> 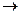 max,
Ax ≤ b, х ≥0 max,
Ax ≤ b, х ≥0
| Стандартная: <b,y> 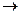 min,
yA ≥ c, y ≥0 min,
yA ≥ c, y ≥0
|
Каноническая:c,x> 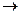 max,
Ax = b, х ≥0 max,
Ax = b, х ≥0
| Основная: <b,y> 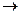 min,
yA ≥ c min,
yA ≥ c
|
Теорема 6.1. Задачи (6.11) и (6.12) взаимодвойственны, т. е. двойственной к задаче (6.12) является задача (6.11).
Ниже под Х и У понимаются допустимые множества задач (6.11) и (6.12) соответственно.
Теорема 6.2.Для любых хÎХ и yÎY выполняется неравенство
<с, х> £ <b, у>.
Теорема 6.3. Пусть х*Î X, у*Î Y. Тогда
1) если
<с, х*> = <b,у*>, (6.13)
то х* есть решение задачи (6.11), а у* — решение задачи (6.12);
2) равенство (6.13) равносильно совокупности условий

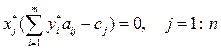 , (6.14)
, (6.14)
 (6.15)
(6.15)
Равенство (6.13) принято называть соотношением двойственности, условия (6.14), (6.15) — условиями дополняющей нежесткости.
Теорема 6.4 (теорема двойственности). Прямая задача (6.11) имеет решение в том и только том случае, если двойственная задача (6.12) имеет решение; при этом значения данных задач совпадают, т. е. для любых их решений х* и у* выполнено соотношение двойственности (6.12).
При практическом применении теории двойственности особенно полезным является следующее утверждение, непосредственно вытекающее из теорем 6.3 и 6.4.
Теорема 6.5 (о дополняющей нежесткости). Точки x*Î Х и у*Î Y являются решениями взаимодвойственных задач (6.11) и (6.12) соответственно в том и только том случае, если выполняются условия (6.14), (6.15).
Итак, взаимодвойственые задачи ЛП имеют или не имеют решения одновременно. Следующая теорема показывает, что уже по их допустимым множествам можно отличить первый случай от второго.
Теорема 6.6. Если допустимые множества взаимодвойственных задач (6.11) и (6.12) непусты, то обе они имеют решение. Если же только у одной из них допустимое множество непусто, то ее значение бесконечно, т. е.
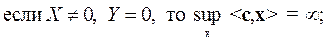

Пример 6.5. Построить задачу двойственную к следующей задаче ЛП.
17х1 - 5 х2 + х3+ х4 - 8х5 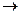 max,
max,
3х1 - х2 - х3 + 4х4 + 7х5 ≤11,
х1 - 5 х2 - 7х3 + х4 + 2х5 ≥-8,
х1 + х2 + х3 + 3х4 – х5=4,
х1 ≥ 0, х4 ≥ 0.
Решение. Составим таблицу перехода к двойственной задаче (табл. 6.3).
Отсюда получаем ответ:
Таблица 6.3
Таблица перехода к двойственной задаче
х1≥0 х2 х3 х4≥0 х5
| y1 ≥0 y2 ≥0 y3 | 3 -1 -1 4 7 -1 5 7 -1 -2 1 1 1 3 -1 | ≤ ≤ = | |
| ≥ = = ≥ = | |||
| 17 -5 1 1 -8 |
11y1 +8y2 + 4y3 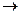 min,
min,
3y1 - y2 + y3 ≥17,
-y1 + 5y2 + y3 = -5,
-y1 + 7y2 + y3 =1,
4y1 - y2 + 3y3 ≥1,
7y1 - 2y2 - y3= -8,
y1≥0, y2 ≥0.