Многомерная минимизация при наличии ограничений

6.1. Линейное программирование

 

Задача минимизации функции n переменных ¦(x) = (x₁,…, x_n) на некотором множестве Х Еⁿ не совпадающая со всем пространством Еⁿ и заданном с помощью ограничений (равенств и неравенств) на координаты х_j (j = 1:n) точки хÎEⁿ называется задачей математического программированияи в общем виде записывается:

X = {x 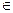Eⁿ|g_i(x) ≤ 0, i = 1:m}.

Математическое программирование −это область математики, разрабатывающая теорию и численные методы решения многомерных задач с ограничениями, т.е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

Частным случаем этих задач, в которых отыскивается минимум или максимум некоторой линейной функции и ограничения представляются в виде равенств и неравенств, все переменные х_j удовлетворяют условию не отрицательности х_j ³0 (j = 1:n) являются задачи линейного программирования (ЛП).

Основные идеи линейного программирования возникли во время второй мировой войны в связи с поиском оптимальных стратегий при ведении военных операций и в дальнейшем были использованы для решения многих задач из области управления, торговли и техники. В частности, линейное программирование широко используется для проектирования радиоэлектронных средств и систем, конструкций и технологических процессов производства радиоаппаратуры.

При проектировании радиоэлектронных средств целевая функция будет характеризовать качество работы, стоимость аппаратуры либо иные характеристики, зависящие от параметров составляющих компонентов, оптимальные значения которых в результате решения задачи необходимо найти. Ограничения представляют собой систему соотношений, сужающих допустимую область изменения параметров компонентов при решении задач оптимизации.

Линейное программирование представляет собой наиболее часто используемый метод оптимизации (74% от общего числа применяемых оптимизационных методов).

6.1.1.Постановка задач линейного программирования

Задача линейного программирования формулируется следующим образом.

Среди точек х= (х₁,…, х_n)ÎEⁿ, удовлетворяющихограничениям:

а_ij x_j £ b_{i ,} i = 1:k; (6.1)

а_ijx_j = b_i , i = (k+1):m; (6.2)

x_j ³ 0, j = 1:n (6.3)

найти те, в которых функция

¦(х) = c_j x_j

принимает минимальное значение, и определить это значение. Это общая или произвольная форма записи.

Отметим, что в условии задачи линейного программирования могут содержаться неравенства и противоположного, чем в (6.2), знака, однако такие неравенства легко сводятся к виду (6.2) умножением на − 1.

Если в условии задачи линейного программирования не содержаться ограничения − равенства (6.1), то эта форма записи называется симметричнойили стандартной.

Если в условии задачи линейного программирования не содержаться ограничения − неравенства (6.2), то есть в (6.1) l = m, то она называется задачей линейного программирования в каноническом (основном) виде.

Ограничения – неравенства

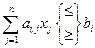
преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) переменных х_n+i ≥ 0, i = 1: k. Ограничения − неравенства (6.2) можно записать в виде равенств:

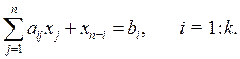
Таким образом, любая задача линейного программирования может быть записана в каноническом виде:

 

f(x) = (6.4)

а_ij x_j = b_{i ,} i = 1:m, (6.5)

x_j ≥ 0, j = 1:n. (6.6)

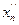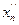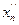Если переменная х_n не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными и , приняв х_n = − , ≥ 0, ≥ 0.

Часто используется векторная записьзадачи (6.3)…(6.5):

f(x) = (c,x) 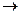min,

Ax = b, (6.7)

х ≥ 0,

где х = (х₁,…, х_n)^Т– векторнезависимых переменных, с= (с₁,…, с_n)^Т – вектор коэффициентов целевой функции из (6.3), А= (а_ij) – прямоугольная матрица размера m´n, b= (b₁,…, b_m)^Т– вектор правых частей (ограничений) системы (6.4), а х³ 0 − краткая запись условий неотрицательности (6.3).

Ограничения вида х_j ≥ 0 или х_j£ 0, или d_j £ x_j£ p_j (двусторонние ограничения) для всех или некоторых j (j = 1:n) называют прямыми ограничениями на переменные. Методы решения задач линейного программирования построены, как правило, с учетом вида прямых ограничений.

Обозначив а_ijx_j = g_i(x), условимся ограничение g_i(x) £ 0 называть активнымв точке x₀, если это неравенство при x = x₀ обращается в равенство, т.е. если g_i(x₀) = 0 . В случае строгого неравенства g_i(x₀) < 0 данное ограничение называют неактивным в точке x₀. На рис. 6.1 изображены точка x₀ , в которой оба ограничения активны, и точка х¢, в которой оба ограничения неактивны.

 

 

 

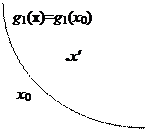
Рис. 6.1. Графическая иллюстрация активного и неактивного ограничений

 

Задача линейного программирования, которая имеет допустимые решения (т.е. система ограничений совместна) называется допустимой; задача с несовместной системой ограничений – недопустимой.

Совокупность чисел х= (х₁,…, х_n), удовлетворяющих ограничениям задачи (6.1)…(6.2), называется допустимым решением (или планом).

План х* = (х₁*,…, х_n*), при котором целевая функция задачи (6.1)…(6.3) принимает свое минимальное (максимальное) значение, называется оптимальным.

Задача математического программирования может иметь не один оптимальный план. Значение целевой функции при любом из оптимальных планов называется оптимумом задачи математического программирования.

Чтобы имело смысл говорить об отыскании оптимального плана задачи система (6.1)…(6.3) должна быть совместна и иметь не единственное неотрицательное решение. Это возможно в случае, если ранг r системы (число линейно независимых уравнений) меньше числа неизвестных n (r < n), при r = n – система допускает единственное решение, и вопрос о выборе оптимального решения отпадает. Случай r > n вообще невозможен.

Пример 6.1. Привести к канонической форме следующие задачи линейного программирования:

а) f(x) = 6х₁ + 5х₂ 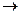min

Решение. Заменяем функцию f(x) на . Из левых частей ограничений типа ≥ вычитаем неотрицательные переменные х₃, х₄, _,х₅, к левым частям ограничений типа ≤ прибавляем неотрицательные переменные х₆, х_7. Получаем модель задачи в канонической форме:

,

б) f(x) = 2х₁ − 3х₂ + 5х₃ − х₄ 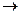max,

 

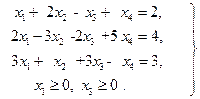
Решение. Эта задача не является канонической из-за того, что не от всех переменных требуется неотрицательность. Представим переменные х₂, х₄ в виде разностей 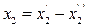, , где 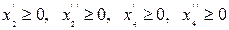. Подставляя эти разности в значение функции и ограничения, получим каноническую задачу:

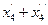
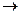f(x) = 2х₁− 3( ) + 5х₃ − max,