Тест Бокса-Кокса в форме Зарембки

Вопрос №13) Классическая линейная модель множественной регрессии (КЛММР). Постановка задачи. Понятие гомоскедастичности регрессионных остатков.

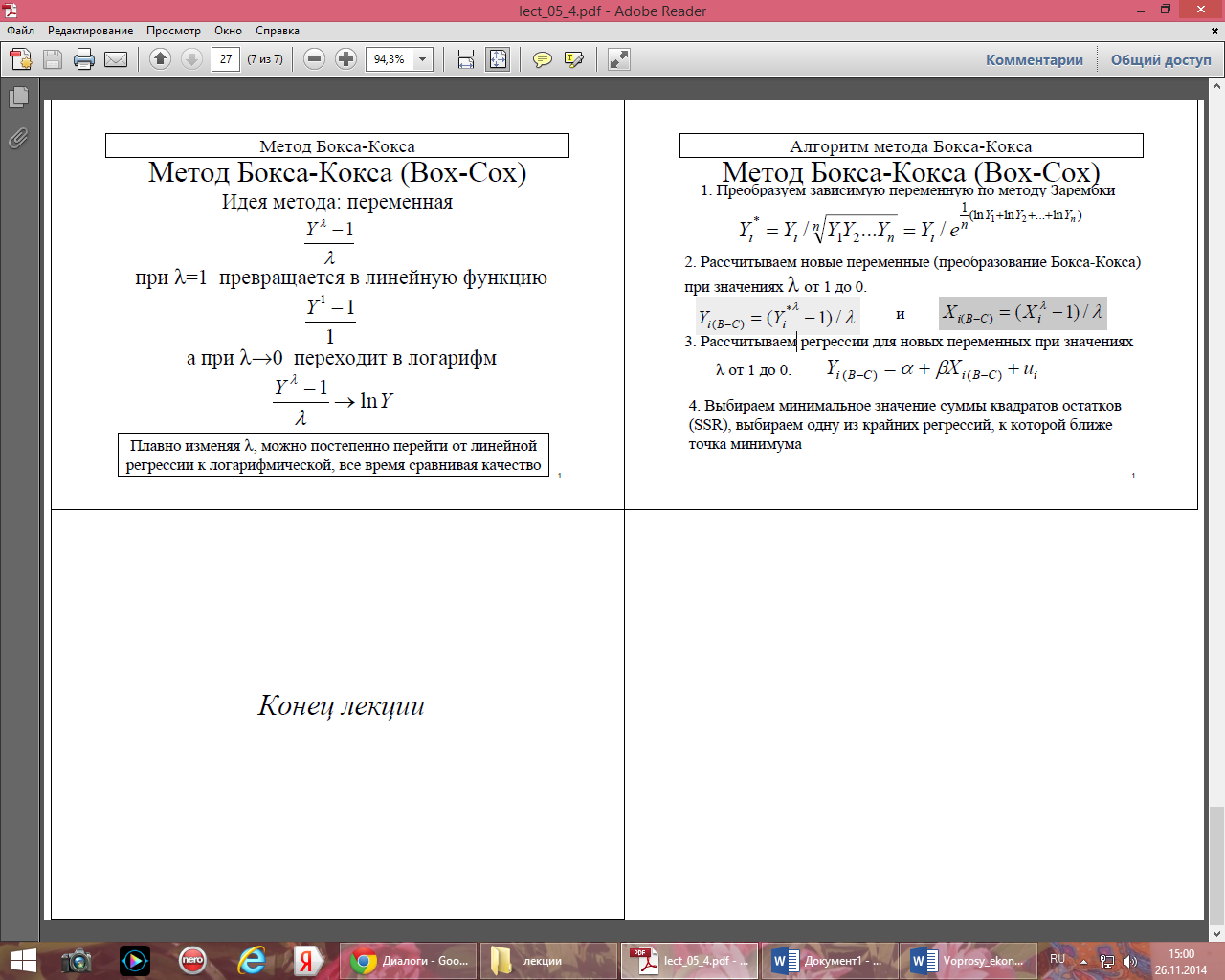
Классическая линейная модель множественной регрессии (КЛММР) представляет собой простейшую версию конкретизации требований к общему виду функции регрессии f(X), природе объясняющих переменных X и статистических регрессионных остатков e(Х) в общих уравнениях регрессионной связи. Процесс конкретизации подобных требований к структуре и характеру анализируемых моделей регрессионного типа обычно называют спецификацией модели

В рамках КЛММР рассматриваются только линейные функции регрессии, т.е.

Теоретическое уравнение линейной модели множественной регрессии

(ЛММР) записывается следующим образом:

где объясняющие переменные x⁽¹⁾, x⁽²⁾,…, x^(p) играют роль неслучайных параметров, от которых зависит закон распределения вероятностей результирующей переменной y. Это, в частности, означает, что в повторяющихся выборочных наблюдениях (x_i⁽¹⁾, x_i⁽²⁾,..., х_i^(p); y_i) единственным источником случайных возмущений значений y_i являются случайные возмущения регрессионных остатков e_i

При k = 1 уравнение становится уравнением парной линейной

регрессии.

Кроме того, постулируется взаимная некоррелированность случайных регрессионных остатков (E(e_ie_j) = 0 для i ¹ j). Это требование к регрессионным остаткамe₁,...,e_n относится к основным предположениям классической модели и оказывается вполне естественным в широком классе реальных ситуаций, особенно, если речь идет о пространственных выборках т.е. о ситуациях, когда значения анализируемых переменных регистрируются на различных объектах (индивидуумах, семьях, предприятиях, банках, регионах и т. п.). В этом случае данное предположение означает, что «возмущения» (регрессионные остатки), получающиеся при наблюдении одного какого-либо обследуемого объекта, не влияют на «возмущения», характеризующие наблюдения над другими объектами, и наоборот.

Тот факт, что для всех остатков e₁,E₂,...,e_n выполняется соотношение Ee_i²; =s², где величина s²от номера наблюдения i не зависит, означает неизменность (постоянство, независимость от того, при каких значениях объясняющих переменных производятся наблюдения) дисперсий регрессионных остатков. Последнее свойство принято называть гомоскедастичностью регрессионных остатков.

Что касается требования к рангу матрицы X, то оно означает, что не должно существовать строгой линейной зависимости между объясняющими переменными. Так, если, например, одна объясняющая переменная может быть линейно выражена через какое-то количество других, то ранг матрицы X окажется меньше р + 1, а следовательно, и ранг матрицы X^TX будет тоже меньше р + 1. А это означает вырождение симметрической матрицы Х^TХ (т.е. det(X^TX) = 0), что исключает существование матрицы (X^TX)^-1 , которая, как мы увидим, играет важную роль в процедуре оценивания параметров анализируемой модели.

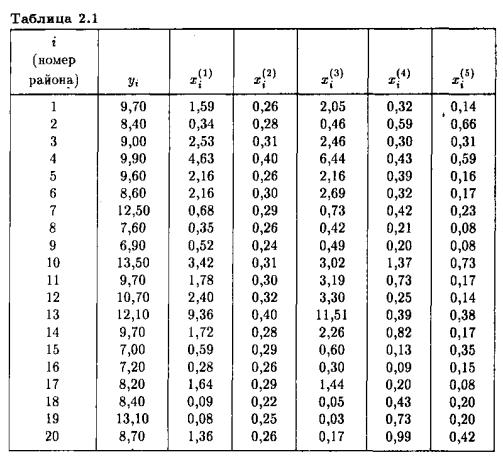
Пример 2.1. Исследуется зависимость урожайности зерновых культур (у ц/га) от ряда переменных, характеризующих различные факторы сельскохозяйственного производства, а именно:

x⁽¹⁾ — число тракторов (приведенной мощности) на 100 га;

x⁽²⁾ — число зерноуборочных комбайнов на 100 га;

x⁽³⁾_ — число орудий поверхностной обработки почвы на 100 га;

x⁽⁴⁾ — количество удобрений, расходуемых на гектар (т/га);

x⁽⁵⁾ — количество химических средств защиты растений, расходуемых на гектар (ц/га).

Исходные данные для 20 сельскохозяйственных районов области приведены в табл. 2.1.

Таким образом, в данном примере мы располагаем пространственной выборкой объема n = 20; число объясняющих переменных р = 5. Матрица X будет составлена из шести столбцов размерности 20 каждый, причем в качестве первого столбца используется вектор, состоящий из одних единиц, а столбцы со 2-го по 6-й представлены соответственно 3-7-м столбцами табл. 2.1. Вектор-столбец Y определяется 2-м столбцом табл. 2.1. Специальный анализ технологии сбора исходных статистических данных показал, что допущение о взаимной некоррелированности и гомоскедастичности регрессионных остатков e может быть принято в качестве рабочей гипотезы. Поэтому мы можем записать уравнения статистической связи между y_i и X_i = (х_i⁽¹⁾, х_i⁽²⁾, x_i⁽³⁾, х_i⁽⁴⁾,х_i⁽⁵⁾)^T

Гомоскелостичность. Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора х остатки Sj имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место ге- тероскедастичность.
При нарушении гомоскедастичности мы имеем неравенства
2 2 2 . s i^S , jФ i.
При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта. Основная идея теста Гольдфель- да- Квандта состоит в следующем:

упорядочение п наблюдений по мере возрастания переменной х; исключение из рассмотрения С центральных наблюдений, при этом (п - С) : 2 > р, где p - число оцениваемых параметров; разделение совокупности из (n - С) наблюдений на две группы (соответственно с малыми и с большими значениями фактора х) и определение по каждой из групп уравнений регрессии; определение остаточной суммы квадратов для первой (51) и второй (52) групп и нахождение их отношения: R = 52 : 51.

При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F-критерию со степенями свободы k1 = (п - С - 2р) : 2, k2 = (п - С - 2р) : 2. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

 

№14 Вопрос.